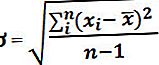دالة POWER في Excel (صيغة ، أمثلة) | كيفية استخدام POWER في Excel
في الرياضيات ، كان لدينا الأسس التي كانت القوة لأي رقم أساسي معين ، في excel لدينا وظيفة داخلية مماثلة تُعرف باسم وظيفة POWER والتي تُستخدم لحساب قوة رقم أو قاعدة معينة ، لاستخدام هذه الدالة يمكننا استخدام الكلمة الأساسية = POWER (في خلية وتقديم وسيطتين إحداهما كرقم والأخرى كقوة.
القوة في Excel
القوة في Excel هي دالة رياضية / مثلثية تحسب وترجع نتيجة رقم مرفوع إلى أس. يأخذ وظيفة السلطة إكسل حجتين في قاعدة (أي عدد حقيقي)، و الأس ( السلطة، وهذا يدل على عدد المرات التي سوف تضاعف عدد معين من قبل نفسه). هذا يعني ، على سبيل المثال ، أن 5 مضروبًا في قوة 2 يساوي 5 × 5.
صيغة وظيفة الطاقة

شرح وظيفة POWER في Excel
تأخذ Power in Excel الوسيطة كقيمة عددية ، ومن ثم تكون الوسائط التي تم تمريرها من نوع عدد صحيح حيث يكون الرقم هو الرقم الأساسي والقوة هي الأس. كلتا الوسيطتين مطلوبة وليست اختيارية.



يمكننا استخدام وظيفة Power في التفوق بعدة طرق ، مثل العمليات الحسابية ومعادلة دالة القدرة ويمكن استخدامها لحساب الدوال الجبرية العلائقية.
كيفية استخدام وظيفة POWER في Excel
وظيفة Excel POWER بسيطة للغاية وسهلة الاستخدام. دعنا نفهم عمل POWER في التفوق ببعض الأمثلة.
يمكنك تنزيل قالب Excel الخاص بوظيفة الطاقة من هنا - قالب Excel الخاص بوظيفة الطاقةPOWER في Excel المثال رقم 1
على سبيل المثال ، لدينا معادلة دالة القوة y = x ^ n (x مرفوعة للقوة n) ، حيث تعتمد y على قيمة x و n هي الأس. نريد أيضًا رسم الرسم البياني للدالة f (x ، y) لقيمتي x و n = 2. قيم x هي:

لذلك ، في هذه الحالة ، نظرًا لأن قيمة y تعتمد على القوة n لـ x ، فسنحسب قيمة Y باستخدام وظيفة POWER في Excel.
- ستكون القيمة الأولى لـ y 2 ^ 2 (= POWER (2،2)
- ستكون القيمة الثانية لـ y 4 ^ 2 (= POWER (4،2)
- ……………………………………………………………………
- ……………………………………………………………………
- ستكون القيمة العاشرة لـ y 10 ^ 2 (= POWER (10،2)

الآن ، حدد قيم x و y من النطاق B4: K5 ، حدد الرسم البياني (في هذا حددنا الرسم البياني المبعثر بخطوط ناعمة) من علامة تبويب الإدراج.

لذلك ، نحصل على رسم بياني أسي خطي لمعادلة دالة POWER المحددة.

POWER في Excel المثال رقم 2
في الجبر ، لدينا معادلة دالة POWER من الدرجة الثانية ، والتي يتم تمثيلها على أنها ax2 + bx + c = 0 ، حيث x غير معروف و a و b و c هي المعاملات. يعطي حل معادلة POWER Function جذور المعادلة التي تمثل قيم x.
تُحسب جذور معادلة دالة الطاقة التربيعية باتباع الصيغة الرياضية
- س = (-b + (b2-4ac) 1/2) / 2a
- س = (-b- (b2-4ac) 1/2) / 2a
يُطلق على b2-4ac كمميز ويصف عدد الجذور التي تمتلكها معادلة دالة POWER من الدرجة الثانية.
الآن ، لدينا قائمة من معادلة دالة POWER من الدرجة الثانية الواردة في العمود A ونحتاج إلى إيجاد جذور المعادلات.

^ يسمى المشغل الأسي المستخدم لتمثيل القوة (الأس). X2 هو نفسه x ^ 2.
لدينا خمس معادلات دالة POWER من الدرجة الثانية وسنحلها باستخدام الصيغة بمساعدة وظيفة POWER في excel لاكتشاف الجذور.
في معادلة دالة POWER الأولى ، a = 4 ، b = 56 ، c = -96 ، إذا قمنا بحلها رياضيًا باستخدام الصيغة أعلاه ، لدينا الجذور -15.5 و 1.5

لتنفيذ هذا في صيغة Excel ، سنستخدم وظيفة POWER في Excel وستكون الصيغة
- = ((- 56 + POWER (POWER (56،2) - (4 * 4 * (- 93))، 1/2))) / (2 * 4) سيعطي الجذر الأول و
- = ((-56-POWER (POWER (56،2) - (4 * 4 * (- 93))، 1/2))) / (2 * 4) ستعطي الجذر الثاني للمعادلة
إذن ، الصيغة الكاملة ستكون ،
= "جذور المعادلات هي" & "" & ((- 56 + POWER (POWER (56،2) - (4 * 4 * (- 93)) ، 1/2))) / (2 * 4) & " ، "& ((- 56-POWER (POWER (56،2) - (4 * 4 * (- 93))، 1/2))) / (2 * 4)
كلا الصيغتين متسلسلة مع سلسلة "جذور المعادلة هي".
باستخدام نفس الصيغة لمعادلة POWER Function الأخرى التي لدينا ،  الإخراج:
الإخراج:
POWER في Excel المثال رقم 3
لذلك ، بالنسبة للحسابات الرياضية المختلفة ، يمكننا استخدام وظيفة POWER في Excel.
لنفترض أنه يتعين علينا إيجاد الفائدة المركبة التي تكون الصيغة لها
المبلغ = الرئيسي (1 + r / n) nt
- حيث r هو معدل الفائدة ، n هو عدد مرات تراكم الفائدة في السنة و t هو الوقت
- إذا تم إيداع مبلغ 4000 دولار في حساب (توفير) بمعدل فائدة 5٪ سنويًا ، مركبًا شهريًا ، يمكن حساب قيمة الاستثمار بعد 5 سنوات باستخدام صيغة الفائدة المركبة أعلاه.
- حيث الأصل = 4000 دولار ، المعدل = 5/100 أي 0.05 ، ن = 12 (مركب شهريًا) ، الوقت = 5 سنوات
باستخدام صيغة الفائدة المركبة وتنفيذها في صيغة excel باستخدام وظيفة POWER في Excel ، لدينا الصيغة
= B2 * (POWER ((1+ (B3 / B5))، (B4 * B5)))

إذن ، رصيد الاستثمار بعد 5 سنوات هو 5.133.43 دولار
POWER في Excel المثال رقم 4
وفقًا لقانون الجاذبية لنيوتن ، جسمان على مسافة r من مركز جاذبيتهما يجذبان بعضهما البعض في الكون وفقًا لصيغة POWER Excel
F = (G * M * م) / r2
حيث F هو مقدار قوة الجاذبية ، و G يسمى ثابت الجاذبية ، و M هي كتلة الجسم الأول و m هي كتلة الجسم الثاني و r هي المسافة بين الأجسام من مركز الجاذبية.
دعونا نحسب مقدار قوة الجاذبية التي تسحب بها الشمس الأرض
- كتلة الشمس 1.98 * 10 ^ 30 كجم
- كتلة الأرض 5.97 * 10 ^ 24 كجم
- تبلغ المسافة بين الشمس والأرض 1.496 × 10 ^ 11 مترًا
- قيمة ثابت الجاذبية هي 6.67 * 10 ^ -11 م 3 كجم -1 ث -2
في Excel ، إذا أردنا حساب قوة الجاذبية ، فسنستخدم مرة أخرى POWER في Excel التي يمكن أن تعمل على قيم رقمية كبيرة.
- لذلك ، باستخدام POWER في Excel ، يمكننا تحويل قيم الترميز العلمي إلى صيغة POWER Excel
- سيتم تمثيل 1.98 * 10 ^ 30 كـ 1.98 * قوة (10،30) ، وبالمثل قيم أخرى.
- لذلك ، فإن صيغة POWER Excel لحساب القوة ستكون = (6.67 * POWER (10، -11) * 1.98 * POWER (10،30) * 5.97 * POWER (10،24)) / POWER (1.496 * POWER (10) ، 11)، 2)

نظرًا لأن القيمة التي تم الحصول عليها كقوة هي رقم كبير ، فقد عبر عنه Excel بالتدوين العلمي. لتغييره إلى كسر ، قم بتغيير التنسيق إلى الكسر
 انتاج:
انتاج:
لذا ، تسحب الشمس الأرض بقوة مقدارها 35229150283107900000000 نيوتن.