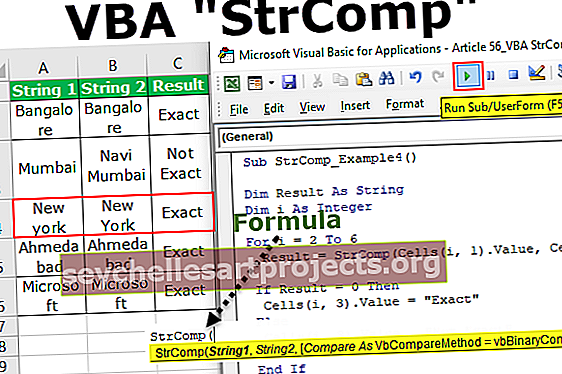
الفرق بين اختبار Z واختبار T لاختبار الفرضيات
الاختلافات بين اختبار Z و اختبار T
اختبار Z هو الفرضية الإحصائية التي يتم استخدامها لتحديد ما إذا كانت العيّنتان تعنيان مختلفتين في حالة توفر الانحراف المعياري وكانت العينة كبيرة بينما يتم استخدام اختبار T لتحديد مدى متوسط مجموعات البيانات المختلفة تختلف عن بعضها البعض في حالة الانحراف المعياري أو عدم معرفة الفرق.
اختبارات Z واختبارات t هما الطريقتان الإحصائيتان اللتان تتضمنان تحليل البيانات التي لها تطبيقات في العلوم والأعمال والعديد من التخصصات الأخرى. يمكن إحالة اختبار t إلى اختبار فرضية أحادية المتغير يعتمد على إحصاء t ، حيث يكون المتوسط ، أي أن المتوسط معروف ، وتباين المجتمع ، أي يتم تقريب الانحراف المعياري من العينة. من ناحية أخرى ، اختبار Z ، وهو أيضًا اختبار أحادي المتغير يعتمد على التوزيع الطبيعي القياسي.

الاستخدامات
# 1 - اختبار Z
صيغة Z-test ، كما ذكرنا سابقًا ، هي الحسابات الإحصائية التي يمكن استخدامها لمقارنة متوسطات السكان بالعينة. سيخبرك z-test بمدى بعد نقطة البيانات ، من حيث الانحرافات المعيارية ، عن متوسط مجموعة البيانات. سيجري اختبار z مقارنة لعينة بمجتمع محدد يستخدم عادةً للتعامل مع المشكلات المتعلقة بالعينات الكبيرة (أي n> 30). في الغالب ، تكون مفيدة جدًا عند معرفة الانحراف المعياري.
# 2 - اختبار T
اختبارات T هي أيضًا حسابات يمكن استخدامها لاختبار الفرضية ، ولكنها مفيدة جدًا عندما نحتاج إلى تحديد ما إذا كانت هناك مقارنة ذات دلالة إحصائية بين مجموعتي العينة المستقلتين. بمعنى آخر ، يسأل اختبار t عما إذا كانت المقارنة بين متوسطات مجموعتين من غير المرجح أن تكون قد حدثت بسبب الصدفة العشوائية. عادةً ما تكون اختبارات t أكثر ملاءمة عندما تتعامل مع مشاكل ذات حجم عينة محدود (أي n <30).
إنفوجرافيك Z-Test مقابل T-Test
نقدم لك هنا أهم 5 اختلافات بين z-test و t-test التي يجب أن تعرفها.

الاختلافات الرئيسية
- أحد أهم الشروط لإجراء اختبار t هو أن الانحراف المعياري للمجتمع أو التباين غير معروف. على العكس من ذلك ، يجب افتراض أن صيغة التباين السكاني كما هو مذكور أعلاه معروفة أو معروفة في حالة اختبار z.
- يعتمد اختبار t كما ذكرنا سابقًا على توزيع t للطالب. على العكس من ذلك ، يعتمد اختبار z على افتراض أن توزيع وسائل العينة سيكون طبيعيًا. يظهر كل من التوزيع الطبيعي وتوزيع t للطالب كما هو ، حيث أن كلاهما على شكل جرس ومتماثل. ومع ذلك ، فإنها تختلف في إحدى الحالات التي في التوزيع ، هناك مساحة أقل في المركز وأكثر في ذيولهم.
- يستخدم اختبار Z على النحو الوارد في الجدول أعلاه عندما يكون حجم العينة كبيرًا ، وهو n> 30 ، ويكون اختبار t مناسبًا عندما لا يكون حجم العينة كبيرًا وهو صغير ، أي أن n <30.
جدول مقارنة Z-Test مقابل T-Test
| أساس | اختبار Z | اختبار T | ||
| التعريف الأساسي | Z-test هو نوع من اختبار الفرضية الذي يتحقق مما إذا كانت متوسطات مجموعتي البيانات مختلفة عن بعضها البعض عند إعطاء الانحراف المعياري أو التباين. | يمكن إحالة اختبار t إلى نوع من الاختبار البارامتري الذي يتم تطبيقه على هوية ، وكيف تختلف متوسطات مجموعتين من البيانات عن بعضها البعض عندما لا يتم إعطاء الانحراف المعياري أو التباين. | ||
| تباين المجتمع | يُعرف تباين المحتوى أو الانحراف المعياري هنا. | تباين المحتوى أو الانحراف المعياري غير معروف هنا. | ||
| حجم العينة | حجم العينة كبير | هنا حجم العينة صغير. | ||
| الافتراضات الرئيسية |
|
|
||
| بناءً على (نوع التوزيع) | على أساس التوزيع الطبيعي. | بناءً على توزيع Student-t. |
استنتاج
إلى حد كبير ، كلا الاختبارين متشابهان تقريبًا ، لكن المقارنة تأتي فقط لشروطهما لتطبيقهما ، مما يعني أن اختبار t يكون أكثر ملاءمة وقابلية للتطبيق عندما لا يزيد حجم العينة عن ثلاثين وحدة. ومع ذلك ، إذا كانت أكبر من ثلاثين وحدة ، فيجب على المرء استخدام اختبار z. وبالمثل ، هناك أيضًا شروط أخرى ، من شأنها أن توضح الاختبار الذي يجب إجراؤه في الموقف.
حسنًا ، هناك أيضًا اختبارات مختلفة مثل اختبار f ، واختبار ثنائي الذيل مقابل وحيد الذيل ، وما إلى ذلك ، يجب على الإحصائيين توخي الحذر أثناء تطبيقها بعد تحليل الموقف ثم تحديد الاختبار الذي يجب استخدامه. يوجد أدناه نموذج مخطط لما ناقشناه أعلاه.