صيغة التركيب المستمر

صيغة التركيب المستمر | أمثلة | آلة حاسبة

ما هو المضاعفة المستمرة؟

المضاعفة المستمرة تحسب الحد الذي يمكن أن تصل عنده الفائدة المركبة عن طريق التعقيد المستمر لفترة غير محددة من الوقت وبالتالي زيادة مكون الفائدة وفي النهاية قيمة المحفظة لإجمالي الاستثمارات

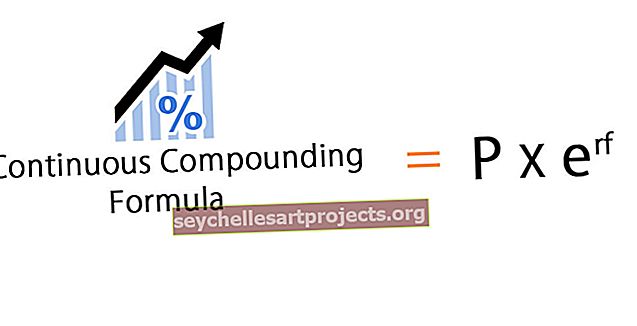
تحدد صيغة التركيب المستمر الفائدة المكتسبة والتي تتضاعف بشكل متكرر لفترة زمنية غير محدودة.

أين،

P = المبلغ الأساسي (القيمة الحالية)
ر = الوقت
r = سعر الفائدة

يفترض الحساب تراكمًا ثابتًا على مدى عدد لا حصر له من الفترات الزمنية. نظرًا لأن الفترة الزمنية غير محدودة ، فإن الأس يساعد في مضاعفة الاستثمار الحالي. يتم ضرب هذا في المعدل والوقت الحاليين. على الرغم من وجود عدد كبير من الاستثمارات ، فإن الاختلاف في إجمالي الفائدة المكتسبة من خلال التفوق المركب المستمر أقل مقارنة بالمركب التقليدي الذي سيتم النظر فيه من خلال الأمثلة.

مثال

دعونا نحلل بعض الحالات:

يمكنك تنزيل قالب Excel المضاعف المستمر هذا من هنا - قالب Excel المضاعف المستمر

إذا تم استثمار مبلغ أولي قدره 1000 دولار أمريكي بفائدة 8٪ سنويًا مع التعقيد المستمر ، فكم سيكون في الحساب بعد 5 سنوات؟

P = 1000 دولار ، ص = 8٪ ، ن = 5 سنوات
FV = P * e rt = 1،000 * e (0.08) (5) = 1،000 * e (0.40) [أُس 0.4 هو 1.491] = 1،000 * 1.491
= 1491.8 دولار

دعونا نحسب تأثيرات نفس الشيء على التركيب المنتظم:

التركيب السنوي:

FV = 1،000 * (1 + 0.08) ^ 1 = 1،080 دولارًا

المركب نصف السنوي:

FV = 1،000 * [(1 + 0.08 / 2)] ^ 2
= 1،000 * (1.04) ^ 2
= 1،000 * 1.0816 = 1،081.60 دولار أمريكي

تجميع ربع سنوي:

FV = 1،000 * [(1 + 0.08 / 4)] ^ 4
= 1،000 * (1.02) ^ 4
= 1،000 * 1.08243
= 1082.43 دولارًا أمريكيًا

التركيب الشهري:

FV = 1،000 * [(1 + 0.08 / 12)] ^ 12
= 1،000 * (1.006) ^ 4
= 1،000 * 1.083
= 1،083 دولارًا أمريكيًا

تفاقم مستمر:

FV = 1،000 * e 0.08
= 1،000 * 1.08328
= 1083.29 دولارًا أمريكيًا

كما يمكن ملاحظته من المثال أعلاه ، فإن الفائدة المكتسبة من التراكم المستمر هي 83.28 دولارًا أمريكيًا ، وهو ما يزيد بمقدار 0.28 دولارًا أمريكيًا عن المركب الشهري.

مثال آخر يمكن أن يقول أن حساب التوفير يدفع فائدة سنوية بنسبة 6٪ ، تتضاعف باستمرار. ما المبلغ الذي يجب استثماره الآن للحصول على 100000 دولار في الحساب بعد 30 عامًا من الآن؟

FV = PV * ert
PV = FV * e - rt
PV = 100،000 * e - (0.06) (30)
PV = 100،000 * e - (1.80)
PV = 100،000 * 0.1652988
PV = 16،529.89 دولارًا

وبالتالي ، إذا تم استثمار مبلغ 16،530 دولارًا (تقريبًا) اليوم ، فسوف ينتج عنه 100000 دولار بعد 30 عامًا بالسعر المحدد.

مثال آخر يمكن أن يكون إذا فرض قرش القرض فائدة بنسبة 80٪ ، مركبة على أساس مستمر ، فما هو معدل الفائدة السنوي الفعلي؟

سعر الفائدة = 0.80 - 1
= 2.2255 - 1 = 1.22.55 = 122.55٪

الاستخدامات

بدلاً من التراكم المستمر للفائدة على أساس شهري أو ربع سنوي أو سنوي ، سيعيد هذا استثمار المكاسب بشكل فعال على الدوام.
يسمح تأثير مبلغ الفائدة بإعادة استثماره مما يسمح للمستثمر بالكسب بمعدل أسي.
يحدد هذا أنه ليس فقط المبلغ الأساسي هو الذي سيكسب المال ، ولكن المضاعفة المستمرة لمبلغ الفائدة ستستمر أيضًا في الضرب.

المستمر يضاعف حاسبة

يمكنك استخدام الحاسبة التالية

ص
ص
ر
الصيغة المركبة المستمرة =

الصيغة المركبة المستمرة =	P xe (rxt) =
	0 * ه (0 * 0) =	0