نسبة شارب | دليل شامل مع أمثلة Excel
تعريف نسبة شارب
نسبة شارب هي النسبة التي طورها William F. Sharpe ويستخدمها المستثمرون من أجل اشتقاق متوسط عائد المحفظة الزائد على معدل العائد الخالي من المخاطر ، لكل وحدة تقلب (الانحراف المعياري) للمحفظة.
خاطئة
تعد نسبة شارب مكونًا مهمًا لتحديد العائدات الإجمالية على المحفظة. هو متوسط العائد المكتسب الذي يزيد عن العائد الخالي من المخاطر مقارنة بالمبلغ الإجمالي للمخاطر التي تتحملها. إنها طريقة لفحص أداء الاستثمار عن طريق تعديل مكون المخاطر الخاص به. تحدد نسبة شارب كيف أن عائد الأصل يعوض المستثمر عن المخاطر التي يتعرض لها. عند مقارنة أصلين مقابل معيار مشترك ، يُشار إلى الأصل الذي يحتوي على نسبة شارب أعلى على أنه فرصة استثمارية مواتية على نفس مستوى المخاطرة.
إذا نظرت إلى الجدول أعلاه ، سترى أن PRWCX لديها نسبة شارب أعلى تبلغ 1.48 وهي أفضل صندوق في مجموعتها.
تعتمد نسبة شارب ، مثل أي نموذج رياضي آخر ، على دقة البيانات التي يجب أن تكون صحيحة. أثناء فحص الأداء الاستثماري للأصول مع تسهيل العوائد ، يمكن اشتقاق نسبة شارب من أداء الأصول الأساسية بدلاً من عوائد الصندوق. غالبًا ما تُستخدم هذه النسبة جنبًا إلى جنب مع نسب ترينور وألفاس لجيسون لتصنيف أداء المحافظ المختلفة أو مديري الصناديق.

معادلة
في عام 1966 ، طور ويليام شارب هذه النسبة التي كانت تسمى في الأصل نسبة "المكافأة إلى التباين" قبل أن يبدأ تسميتها بنسبة شارب من قبل الأكاديميين والمشغلين الماليين اللاحقين. تم تعريفه بطرق متعددة حتى النهاية تم رسمه على النحو التالي:
معادلة النسبة الحادة = (العائد المتوقع - معدل العائد الخالي من المخاطر) / الانحراف المعياري (التقلب)
بعض المفاهيم التي نحتاج إلى فهمها هي:
- العوائد - يمكن أن تكون العوائد بترددات مختلفة مثل اليومية أو الأسبوعية أو الشهرية أو السنوية طالما أن التوزيع منتشر بشكل طبيعي لأن هذه العوائد يمكن أن تكون سنوية للوصول إلى نتائج دقيقة. المواقف غير الطبيعية مثل القمم العالية ، يمكن أن يكون الانحراف في التوزيع مشكلة بالنسبة للنسبة حيث لا يمتلك الانحراف المعياري نفس الفعالية عند وجود هذه المشكلات.
- معدل العائد الخالي من المخاطر - يستخدم هذا لتقييم ما إذا كان الشخص يتم تعويضه بشكل صحيح عن المخاطر الإضافية التي يتحملها بسبب الأصول الخطرة. تقليديا ، معدل العائد بدون خسارة مالية هو الأوراق المالية الحكومية ذات المدة الأقصر (مثل سندات الخزانة الأمريكية). في حين أن مثل هذا النوع من الأوراق المالية لديه أقل قدر من التقلب ، يمكن القول بأن مثل هذه الأوراق المالية يجب أن تتطابق مع الأوراق المالية الأخرى ذات المدة المعادلة.
- الانحراف المعياري - هي كمية تعبر عن عدد الوحدات من مجموعة معينة من المتغيرات التي تختلف عن المتوسط المتوسط للمجموعة. بمجرد حساب هذا العائد الزائد على العائد الخالي من المخاطر ، يجب تقسيمه على الانحراف المعياري للأصل المحفوف بالمخاطر الذي يتم قياسه. كلما زاد العدد ، سيظهر الاستثمار جذابًا من منظور المخاطرة / العائد. ومع ذلك ، ما لم يكن الانحراف المعياري كبيرًا إلى حد كبير ، فقد لا يؤثر مكون الرافعة المالية على النسبة. يمكن مضاعفة كل من البسط (العائد) والمقام (الانحراف المعياري) بدون مشاكل.
مثال
يحتفظ العميل "أ" حاليًا بمبلغ 450.000 دولار أمريكي مستثمر في محفظة مع عائد متوقع بنسبة 12٪ وتقلب بنسبة 10٪. المحفظة الفعالة لديها عائد متوقع بنسبة 17٪ وتقلب بنسبة 12٪. معدل الفائدة الخالي من المخاطر هو 5٪. ما هي نسبة شارب؟
معادلة النسبة الحادة = (العائد المتوقع - معدل العائد الخالي من المخاطر) / الانحراف المعياري (التقلب)
نسبة شارب = (0.12-0.05) /0.10 = 70٪ أو 0.7x
حساب نسبة شارب في Excel
الآن بعد أن عرفنا كيف تعمل الصيغة ، دعونا نحسب نسبة شارب في إكسل.
الخطوة 1 - احصل على المرتجعات بتنسيق جدولي
تتضمن الخطوة الأولى الترتيب لعوائد محفظة الصندوق المشترك الذي تريد تحليله. يمكن أن تكون الفترة الزمنية شهرية أو ربع سنوية أو سنوية. يقدم الجدول أدناه العوائد السنوية للصندوق المشترك.

الخطوة 2 - احصل على تفاصيل الإرجاع الخالية من المخاطر في الجدول
في هذا الجدول أدناه ، افترضت أن العائد الخالي من المخاطر هو 3.0٪ على مدار 15 عامًا. ومع ذلك ، قد يتغير السعر الخالي من المخاطر كل عام وتحتاج إلى وضع هذا الرقم هنا.

الخطوة 3 - البحث عن العائد الزائد
الخطوة الثالثة في حساب نسبة شارب في إكسل هي إيجاد فائض عوائد المحفظة. في حالتنا ، العائد الزائد هو العوائد السنوية - عائد خالي من المخاطر.
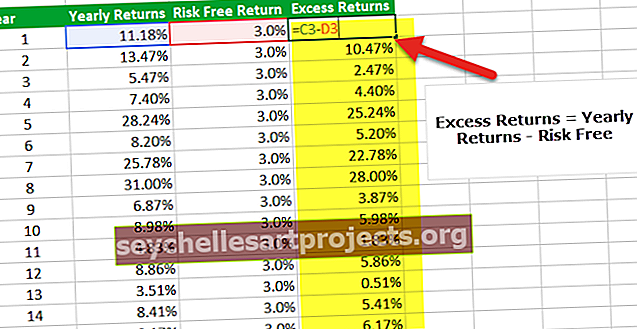
الخطوة 4 - أوجد متوسط العوائد السنوية.
الخطوة الرابعة في حساب نسبة شارب في Excel هي إيجاد متوسط العوائد السنوية. يمكنك استخدام صيغة Excel AVERAGE للعثور على متوسط الحافظة. في مثالنا ، نحصل على متوسط عائد يبلغ 12.09٪.

الخطوة 5 - ابحث عن الانحراف المعياري للعوائد الزائدة
من أجل العثور على الانحراف المعياري للعوائد الزائدة ، يمكنك استخدام صيغة Excel STDEV كما هو موضح أدناه.

الخطوة 6 - حساب نسبة شارب
الخطوة الأخيرة لحساب نسبة شارب في التفوق هي قسمة متوسط العوائد على الانحراف المعياري. نحصل على النسبة = 12.09٪ / 8.8٪ = 1.37x
نحصل على النسبة = 12.09٪ / 8.8٪ = 1.37x

مزايا استخدام نسبة شارب
# 1 - تساعد نسبة شارب في مقارنة ومقارنة إضافة الأصول الجديدة
يتم استخدامه لمقارنة التباين في ميزات المخاطر والعودة الإجمالية للمحفظة كلما تمت إضافة أصل جديد أو فئة من الأصول إليها.
- على سبيل المثال ، يدرس مدير المحفظة إضافة تخصيص صندوق سلع إلى محفظته الاستثمارية الحالية 80/20 من الأسهم التي تبلغ نسبة شارب 0.81.
- إذا كان تخصيص المحفظة الجديدة هو 40/40/20 من الأسهم والسندات وتخصيص صندوق الدين ، فإن نسبة شارب ترتفع إلى 0.92.
هذا مؤشر على أنه على الرغم من أن استثمار صندوق السلع الأساسية متقلب باعتباره تعرضًا قائمًا بذاته ، إلا أنه في هذه الحالة يؤدي في الواقع إلى تحسين خاصية المخاطرة والعائد للمحفظة المدمجة ، وبالتالي يضيف ميزة التنويع في أصل آخر فئة للمحفظة الحالية. يجب أن يكون هناك تدخل في تحليل دقيق بأن تخصيص الأموال قد يحتاج إلى تغيير في مرحلة لاحقة إذا كان له تأثير سلبي على سلامة المحفظة. إذا أدت إضافة الاستثمار الجديد إلى انخفاض النسبة ، فلا ينبغي إدراجه في المحفظة.
# 2 - تساعد نسبة شارب في مقارنة عائد المخاطر
يمكن أن توفر هذه النسبة أيضًا إرشادات حول ما إذا كانت العوائد المفرطة للمحفظة ترجع إلى اتخاذ قرارات استثمارية دقيقة أو نتيجة لمخاطر لا داعي لها تم التعرض لها. على الرغم من أن الصندوق الفردي أو المحفظة يمكن أن يتمتع بعائدات أكبر من أقرانه ، إلا أنه استثمار معقول فقط إذا لم تكن تلك العوائد الأعلى مصحوبة بمخاطر لا داعي لها. كلما زادت نسبة شارب للمحفظة ، كان أداؤها أفضل في أخذ عنصر المخاطر في الاعتبار. تشير نسبة شارب السلبية إلى أن الأصل الأقل خطورة من شأنه أن يؤدي بشكل أفضل من الأمان الذي يتم تحليله.
دعونا نأخذ مثالا على مقارنة المخاطر والعائد.
افترض أن المحفظة A لديها أو من المتوقع أن يكون لها معدل عائد بنسبة 12 ٪ مع انحراف معياري قدره 0.15. بافتراض عائد مرجعي يبلغ حوالي 1.5٪ ، فإن معدل العائد (R) سيكون 0.12 ، و Rf سيكون 0.015 و 's' سيكون 0.15. ستتم قراءة النسبة على أنها (0.12 - 0.015) /0.15 والتي يتم حسابها على 0.70. ومع ذلك ، سيكون هذا الرقم منطقيًا عند مقارنته بمحفظة أخرى مثل المحفظة "ب"
إذا أظهرت المحفظة "ب" تنوعًا أكبر من المحفظة "أ" ولكن لها نفس العائد ، فسيكون لها انحراف معياري أكبر مع نفس معدل العائد من المحفظة. بافتراض أن الانحراف المعياري للمحفظة B هو 0.20 ، ستُقرأ المعادلة على أنها (0.12 - 0.015) / 0.15. ستكون نسبة شارب لهذه المحفظة 0.53 وهي أقل مقارنة بالمحفظة "أ". قد لا تكون هذه نتيجة مذهلة ، مع الأخذ في الاعتبار حقيقة أن كلا الاستثمارين كانا يقدمان نفس العائد ، لكن "ب" كان له قدر أكبر من المخاطرة. من الواضح أن الخيار الذي يحتوي على مخاطر أقل ويقدم نفس العائد سيكون الخيار المفضل.
انتقادات لنسبة شارب
تستخدم نسبة شارب الانحراف المعياري للعوائد في المقام كبديل لمخاطر المحفظة الإجمالية ، مع افتراض أن العوائد موزعة بالتساوي. أظهرت الاختبارات السابقة أن العائدات من بعض الأصول المالية قد تنحرف عن التوزيع الطبيعي ، مما يؤدي إلى تفسيرات ذات صلة لنسبة شارب لتكون مضللة.
يمكن تحسين هذه النسبة من قبل مديري الصناديق المختلفين الذين يحاولون تعزيز عائدهم الظاهري المعدل حسب المخاطر والذي يمكن تنفيذه على النحو التالي:
- زيادة المدة الزمنية المطلوب قياسها : سيؤدي ذلك إلى تقليل احتمالية التقلب. على سبيل المثال ، يكون الانحراف المعياري السنوي للعائدات اليومية أعلى عمومًا من العوائد الأسبوعية ، والتي بدورها أعلى من تلك الخاصة بالعائدات الشهرية. كلما زادت المدة الزمنية ، يجب على المرء أن يستبعد أي عوامل غير متكررة يمكن أن تؤثر على الأداء العام.
- مضاعفة العوائد الشهرية مع حساب الانحراف المعياري باستثناء هذا العائد الشهري المركب المحسوب مؤخرًا.
- كتابة قرارات البيع والشراء خارج نطاق المال للمحفظة: يمكن لمثل هذه الاستراتيجية أن تزيد العوائد عن طريق جمع علاوة الخيارات دون سدادها لعدد من السنوات. تمتلك الاستراتيجيات التي تنطوي على تحدي مخاطر التخلف عن السداد أو مخاطر السيولة أو الأشكال الأخرى من المخاطر واسعة الانتشار نفس القدرة على الإبلاغ عن نسبة شارب المنحازة تصاعديًا.
- تسهيل العوائد: يمكن أن يؤدي استخدام هياكل مشتقة معينة ، أو وضع علامات غير منتظمة على الأصول الأقل سيولة في السوق ، أو استخدام نماذج تسعير معينة تقلل من الأرباح أو الخسائر الشهرية ، إلى تقليل التقلبات المتوقعة.
- القضاء على العوائد المتطرفة: يمكن أن تزيد العوائد المرتفعة جدًا أو المنخفضة جدًا من الانحراف المعياري المبلغ عنه لأي محفظة نظرًا لأنها المسافة من المتوسط. في مثل هذه الحالة ، قد يختار مدير الصندوق التخلص من النهايات القصوى (الأفضل والأسوأ) للعائدات الشهرية كل عام لتقليل الانحراف المعياري والتأثير على النتائج لأن مثل هذا الموقف لمرة واحدة يمكن أن يؤثر على المتوسط العام.
نسبة شارب السابقة واللاحقة
تمت مراجعة نسبة شارب عدة مرات ، لكن هناك شكلين عامين تم استخدامهما مسبقًا (التنبؤ بالعائد والتباين في المستقبل) واللاحق (تحليل تباين العائد السابق).
- تعد توقعات نسبة شارب السابقة سهلة لتقدير الأنماط بعد ملاحظات الأداء السابق لأنشطة استثمارية مماثلة.
- تقيس نسبة Ex-post Sharpe Ratio مدى ارتفاع العائدات ، مقابل مدى تنوع تلك العوائد خلال فترة زمنية معينة. وبشكل أكثر تحديدًا ، هي نسبة العوائد التفاضلية (الفرق بين عوائد الاستثمار والاستثمار القياسي) مقابل التباين التاريخي (الانحراف المعياري) لتلك العوائد.
استنتاج
نسبة شارب هي مقياس قياسي لأداء المحفظة. نظرًا لبساطته وسهولة تفسيره ، فهو أحد أكثر الفهارس شيوعًا. لسوء الحظ ، ينسى معظم المستخدمين الافتراضات التي تؤدي إلى نتيجة غير مناسبة. يجب أن تفكر في التحقق من توزيع العوائد أو التحقق من صحة النتائج بمقاييس أداء مكافئة قبل الوصول إلى قرار بشأن السوق.