صيغة تباين المحفظة (مثال) | كيف تحسب تباين المحفظة؟
ما هو تباين المحفظة؟
يشير مصطلح "تباين المحفظة" إلى القيمة الإحصائية لنظرية الاستثمار الحديثة التي تساعد في قياس تشتت متوسط عوائد المحفظة من وسطها. باختصار ، إنها تحدد إجمالي مخاطر المحفظة. يمكن اشتقاقه بناءً على المتوسط المرجح للتباين الفردي والتغاير المتبادل.
صيغة تباين المحفظة
رياضيا ، يتم تمثيل صيغة تباين المحفظة المكونة من أصلين على النحو التالي ،
صيغة تباين المحفظة = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + 2 * ρ 1،2 * w 1 * w 2 * ơ 1 * ơ 2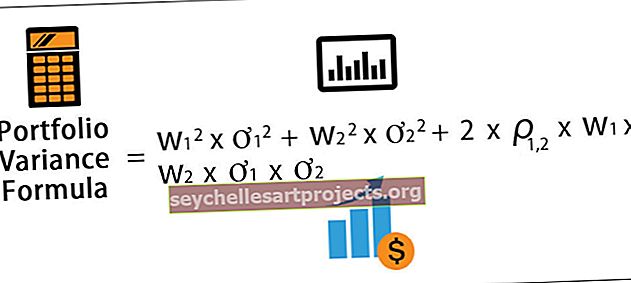
أين،
- w i = وزن حافظة الأصول i
- ơ i 2 = التباين الفردي للأصل i
- ρ i، j = الارتباط بين الأصل i والأصل j
مرة أخرى ، يمكن تمديد الفرق إلى محفظة لا أكثر. من الأصول ، على سبيل المثال ، يمكن تمثيل محفظة 3 أصول على النحو التالي ،
صيغة تباين المحفظة = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + w 3 2 * ơ 3 2 + 2 * ρ 1،2 * w 1 * w 2 * ơ 1 * ơ 2 + 2 * ρ 2،3 * عرض 2 * عرض 3 * ơ 2 * ơ 3 + 2 * ρ 3،1 * عرض 3 * عرض 1 * ơ 3* ơ 1
شرح معادلة تباين المحفظة
يمكن اشتقاق معادلة تباين المحفظة لمحفظة معينة باتباع الخطوات التالية:
الخطوة 1: أولاً ، حدد وزن كل أصل في المحفظة الإجمالية ويتم حسابه بقسمة قيمة الأصول على القيمة الإجمالية للمحفظة. يُشار إلى وزن الأصل بواسطة w i .
الخطوة 2: بعد ذلك ، حدد الانحراف المعياري لكل أصل ويتم حسابه على أساس متوسط العائد الفعلي لكل أصل. يشار إلى الانحراف المعياري للأصل i بالرمز ơ i . مربع الانحراف المعياري هو التباين أي ơ i 2.
الخطوة 3: بعد ذلك ، حدد الارتباط بين الأصول ويلتقط بشكل أساسي حركة كل أصل بالنسبة إلى أصل آخر. يتم الإشارة إلى الارتباط بواسطة ρ.
الخطوة 4: أخيرًا ، يتم اشتقاق معادلة تباين المحفظة لأصلين بناءً على المتوسط المرجح للتباين الفردي والتغاير المشترك كما هو موضح أدناه.
صيغة تباين المحفظة = w 1 * ơ 1 2 + w 2 * ơ 2 2 + 2 * ρ 1،2 * w 1 * w 2 * ơ 1 * ơ 2
مثال على صيغة تباين المحفظة (مع قالب Excel)
يمكنك تنزيل نموذج Excel لصيغة تباين المحفظة من هنا - نموذج Excel لصيغة تباين المحفظة
لنأخذ مثال المحفظة التي تتكون من سهمين. تبلغ قيمة المخزون أ 60 ألف دولار وانحرافه المعياري 15٪ ، بينما قيمة المخزون ب 90 ألف دولار وانحرافه المعياري 10٪. هناك علاقة ارتباط مقدارها 0.85 بين السهمين. حدد التباين.
معطى،
- الانحراف المعياري للمخزون A، ơ A = 15٪
- الانحراف المعياري للمخزون B ، ơ B = 10٪
الارتباط ، ρ أ ، ب = 0.85
يوجد أدناه بيانات لحساب تباين المحفظة لمخزونين.

وزن المخزون أ ، ث أ = 60 ألف دولار / (60 ألف دولار + 90 ألف دولار) * 100٪

وزن المخزون أ = 40٪ أو 0.40
وزن المخزون B ، w B = 90.000 دولار / (60.000 دولار + 90.000 دولار) * 100٪

وزن المخزون ب = 60٪ أو 0.60
لذلك ، سيكون حساب فرق المحفظة على النحو التالي ،

الفرق = w A 2 * ơ A 2 + w B 2 * ơ B 2 + 2 * ρ A، B * w A * w B * ơ A * ơ B
= 0.4 ^ 2 * (0.15) 2 + 0.6 ^ 2 * (0.10) 2 + 2 * 0.85 * 0.4 * 0.6 * 0.15 * 0.10

لذلك ، يكون التباين 1.33٪.
الصلة والاستخدام
واحدة من السمات الأكثر لفتًا للانتباه في المحفظة هي حقيقة أن قيمتها مشتقة على أساس المتوسط المرجح للفروق الفردية لكل من الأصول المعدلة حسب تغايراتها. يشير هذا إلى أن التباين العام أقل من المتوسط المرجح البسيط للفروق الفردية لكل سهم في المحفظة. وتجدر الإشارة إلى أن المحفظة التي تحتوي على أوراق مالية ذات ارتباط أقل فيما بينها ، ينتهي بها الأمر بتباين أقل في المحفظة.
يعد فهم معادلة تباين المحفظة أمرًا مهمًا أيضًا لأنه يجد تطبيقًا في نظرية المحفظة الحديثة المبنية على الافتراض الأساسي بأن المستثمرين العاديين يعتزمون تعظيم عائداتهم مع تقليل المخاطر ، مثل التباين. يسعى المستثمر عادة إلى ما يسمى بالحدود الفعالة ، وهو أدنى مستوى من المخاطرة أو التقلب يمكن للمستثمر من خلاله تحقيق عائده المستهدف. في أغلب الأحيان ، يستثمر المستثمرون في أصول غير مرتبطة لتقليل المخاطر وفقًا لنظرية المحفظة الحديثة.
هناك حالات يمكن فيها للأصول التي قد تكون محفوفة بالمخاطر بشكل فردي أن تقلل في النهاية من تباين المحفظة لأن مثل هذا الاستثمار من المرجح أن يرتفع عندما تنخفض الاستثمارات الأخرى. على هذا النحو ، يمكن أن يساعد هذا الارتباط المنخفض في تقليل تباين المحفظة الافتراضية. عادة ، يتم قياس مستوى مخاطر المحفظة باستخدام الانحراف المعياري ، والذي يتم حسابه على أنه الجذر التربيعي للتباين. من المتوقع أن يظل التباين مرتفعًا عندما تكون نقاط البيانات بعيدة عن المتوسط ، مما يؤدي في النهاية إلى مستوى إجمالي أعلى من المخاطر في المحفظة أيضًا.