مربع R المعدل (المعنى ، الصيغة) | احسب المعدل R ^ 2
ما هو مربع R المعدل؟
يشير المعدل R Squared إلى الأداة الإحصائية التي تساعد المستثمرين في قياس مدى تباين المتغير الذي يعتمد على المتغير والذي يمكن تفسيره بالمتغير المستقل ويأخذ في الاعتبار تأثير المتغيرات المستقلة فقط التي لها تأثير على التباين من المتغير التابع.
يحدد R المعدل أو المعدل R ^ 2 مدى تباين المتغير التابع الذي يمكن تفسيره بواسطة المتغير المستقل. إن تخصص R ^ 2 المعدل هو أنه لا يأخذ في الاعتبار تأثير جميع المتغيرات المستقلة بدلاً من فقط تلك التي تؤثر على تباين المتغير التابع. يمكن أن تكون قيمة R ^ 2 المعدلة سالبة أيضًا ، على الرغم من أنها ليست سلبية في معظم الأوقات.
صيغة R التربيعية المعدلة
يتم تمثيل الصيغة لحساب مربع الانحدار R المعدل على النحو التالي ،
R ^ 2 = {(1 / N) * Σ [(xi - x) * (yi - y)] / (σx * σy)} ^ 2
أين
- R ^ 2 = مربع R المعدل لمعادلة الانحدار
- N = عدد المشاهدات في معادلة الانحدار
- Xi = المتغير المستقل لمعادلة الانحدار
- X = متوسط المتغير المستقل لمعادلة الانحدار
- Yi = المتغير التابع لمعادلة الانحدار
- Y = متوسط المتغير التابع لمعادلة الانحدار
- σx = الانحراف المعياري للمتغير المستقل
- σy = الانحراف المعياري للمتغير التابع.
يرجى الملاحظة
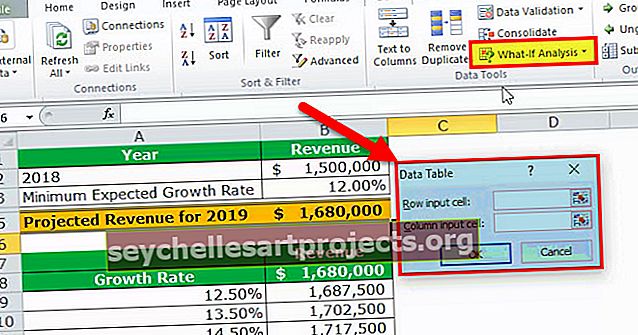
لحسابها في Excel ، يجب توفير متغيري y و x في Excel ويتم إنشاء الإخراج بالكامل مع R ^ 2 المعدلة بواسطة Excel. إنها حالة خاصة يصعب فيها توفير الإخراج بتنسيق نصي ، على عكس الصيغ الأخرى.
ترجمة
مربع R المعدل ، يحدد مدى تباين المتغير التابع الذي يمكن تفسيره بواسطة المتغير المستقل. بالنظر إلى قيمة R ^ 2 المعدلة ، يمكن للمرء أن يقرر ما إذا كانت البيانات الموجودة في معادلة الانحدار مناسبة أم لا. كلما زادت قيمة R ^ 2 المعدلة ، كانت معادلة الانحدار أفضل لأنها تعني أن المتغير المستقل المختار من أجل تحديد المتغير التابع قادر على شرح التباين في المتغير التابع.
يمكن أن تكون قيمة R ^ 2 المعدلة سالبة أيضًا ، على الرغم من أنها ليست سلبية في معظم الأوقات. في حالة مربع R المعدل ، سترتفع قيمة مربع R المعدل مع إضافة متغير مستقل فقط عندما يؤثر تغير المتغير المستقل على التباين في المتغير التابع. هذا لا ينطبق في حالة R ^ 2 ، ينطبق فقط على قيمة R ^ 2 المعدلة.
أمثلة
يمكنك تنزيل قالب Excel المعدل R التربيعي هذا هنا - قالب Excel المعدل R التربيعيمثال 1
دعونا نحاول فهم مفهوم R ^ 2 المعدل بمساعدة مثال. دعونا نحاول معرفة العلاقة بين المسافة التي قطعها سائق الشاحنة وعمر سائق الشاحنة. يقوم شخص ما بالفعل بمعادلة الانحدار للتحقق مما إذا كان ما يعتقده في العلاقة بين متغيرين ، يتم التحقق منه أيضًا من خلال معادلة الانحدار.
في هذا المثال بالذات ، سنرى أي متغير هو المتغير التابع وأي متغير هو المتغير المستقل. المتغير التابع في معادلة الانحدار هذه هو المسافة التي قطعها سائق الشاحنة والمتغير المستقل هو عمر سائق الشاحنة. من خلال إجراء الانحدار باستخدام المتغيرات ، حصلنا على مربع R المعدل ليكون 65٪. اللقطة أدناه تصور ناتج الانحدار للمتغيرات. يتم عرض مجموعة البيانات والمتغيرات في ورقة إكسل المرفقة.

تشير قيمة R ^ 2 المعدلة البالغة 65٪ لهذا الانحدار إلى أن 65٪ من التباين في المتغير التابع يتم تفسيره بواسطة المتغير المستقل. من الناحية المثالية ، سيبحث الباحث عن معامل التحديد الأقرب إلى 100٪.
المثال رقم 2
دعونا نحاول فهم مفهوم مربع R المعدل بمساعدة مثال آخر. دعونا نحاول معرفة العلاقة بين ارتفاع طلاب الفصل ودرجة المعدل التراكمي لهؤلاء الطلاب. في هذا المثال بالذات ، سنرى أي متغير هو المتغير التابع وأي متغير هو المتغير المستقل. المتغير التابع في معادلة الانحدار هو المعدل التراكمي للطلاب والمتغير المستقل هو ارتفاع الطلاب.
من خلال إجراء الانحدار مع المتغيرات ، حصلنا على R ^ 2 المعدلة لتكون ضئيلة أو سالبة. اللقطة أدناه تصور ناتج الانحدار للمتغيرات. يتم عرض مجموعة البيانات والمتغيرات في ورقة إكسل المرفقة.

قيمة R ^ 2 المعدلة لا تذكر لهذا الانحدار مما يعني أن التباين في المتغير التابع لا يفسر بواسطة المتغير المستقل. من الناحية المثالية ، سيبحث الباحث عن معامل التحديد الأقرب إلى 100٪.
ترجمة
يعد مربع R المعدل ناتجًا مهمًا للغاية لمعرفة ما إذا كانت مجموعة البيانات مناسبة أم لا. يقوم شخص ما بالفعل بمعادلة انحدار للتحقق مما إذا كان ما يعتقده في العلاقة بين متغيرين ، يتم التحقق منه أيضًا من خلال معادلة الانحدار. كلما زادت القيمة ، كانت معادلة الانحدار أفضل لأنها تعني أن المتغير المستقل الذي تم اختياره لتحديد المتغير التابع يتم اختياره بشكل صحيح. من الناحية المثالية ، سيبحث الباحث عن معامل التحديد الأقرب إلى 100٪.