الوسط التوافقي (التعريف ، الصيغة) | كيفية حساب؟
ما هو معنى الهارمونيك؟
المتوسط التوافقي هو المقابل للمتوسط الحسابي للمعاملة بالمثل ، أي يتم حساب المتوسط بقسمة عدد الملاحظات في مجموعة البيانات المعطاة على مجموع التبادلات (1 / Xi) لكل ملاحظة في مجموعة البيانات المحددة.
صيغة الوسط التوافقي
المتوسط التوافقي = n / ∑ [1 / X i ]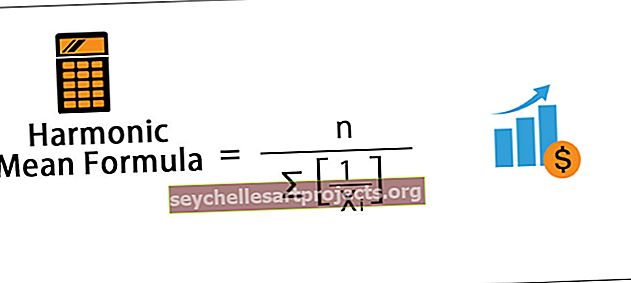
- يمكن للمرء أن يرى أنه مقلوب للمتوسط العادي.
- المتوسط التوافقي للمتوسط العادي هو x / n لذلك إذا تم عكس الصيغة تصبح n / ∑x ومن ثم فإن جميع قيم المقام التي يجب استخدامها يجب أن تكون متبادلة ، أي بالنسبة للبسط يبقى "n" ولكن بالنسبة لـ قاسم القيم أو الملاحظات الخاصة بهم التي نحتاج إلى استخدامها لقيم متبادلة.
- ستكون القيمة المشتقة دائمًا أقل من المتوسط أو تذكر المتوسط الحسابي.
أمثلة
يمكنك تنزيل نموذج Excel للصيغة التوافقية المتناسقة هنا - نموذج Excel لصيغة Harmonic Meanمثال 1
ضع في اعتبارك مجموعة بيانات من الأرقام التالية: 10 ، 2 ، 4 ، 7. باستخدام الصيغة المذكورة أعلاه ، يلزمك حساب المتوسط التوافقي.
المحلول:
استخدم البيانات التالية للحساب.


المتوسط التوافقي = n / ∑ [1 / X i ]
= 4 / (1/10 + 1/2 + 1/4 + 1/7)
= 4 / 0.99

المثال رقم 2
السيد فيجاي محلل أسهم في جي بي مورغان. طلب منه مديره تحديد نسبة السعر إلى الربحية للمؤشر الذي يتتبع أسعار أسهم الشركة W ، والشركة X ، والشركة Y. وتبلغ الشركة W عن أرباح قدرها 40 مليون دولار وقيمة السوق تبلغ 2 مليار دولار ، وتبلغ الشركة X عن أرباحها 3 مليار دولار وقيمة السوق 9 مليار دولار ، بينما تبلغ الشركة Y أرباحًا قدرها 10 مليار دولار وقيمة سوقية تبلغ 40 مليار دولار. احسب المتوسط التوافقي لنسبة السعر إلى العائد للمؤشر.
المحلول:
استخدم البيانات التالية للحساب

أولاً ، يجب أن نحسب نسبة السعر إلى العائد
نسبة السعر إلى العائد هي أساسًا (القيمة السوقية / الأرباح).
- مكرر الربحية (الشركة W) = (2 مليار دولار) / (40 مليون دولار) = 50
- مكرر الربحية (الشركة X) = (9 مليار دولار) / (3 مليار دولار) = 3
- مكرر الربحية (الشركة ص) = (40 مليار دولار) / (10 مليار دولار) = 4
حساب قيمة 1 / X
- الشركة W = 1/50 = 0.02
- الشركة X = 1/3 = 0.33
- الشركة ص = 1/4 = 0.25
يمكن إجراء الحساب على النحو التالي ،

المتوسط التوافقي = n / ∑ [1 / X i ]
- = 3 / (1/50 + 1/3 + 1/4)
- = 3 / 0.60

المثال رقم 3
راي ، أحد سكان شمال كاليفورنيا ، هو سائق دراجة نارية محترف ويقوم بجولته إلى الشاطئ من منزله مساء الأحد حوالي الساعة 5:00 مساءً بتوقيت شرق الولايات المتحدة. يقود دراجته الرياضية بسرعة 50 ميلاً في الساعة للنصف الأول من الرحلة و 70 ميلاً في الساعة للنصف الثاني من منزله إلى الشاطئ. ماذا سيكون متوسط سرعته؟
المحلول:
استخدم البيانات التالية للحساب.

في هذا المثال ، انطلقت راي في رحلة بسرعة معينة وهنا سيعتمد المتوسط على المسافة.
يمكن إجراء الحساب على النحو التالي ،

هنا ، يمكننا حساب المتوسط التوافقي لمتوسط سرعة دراجة Rey الرياضية.
المتوسط التوافقي = n / ∑ [1 / X i ]
- = 2 / (1/50 + 1/70)
- = 2 / 0.03

متوسط سرعة دراجة راي الرياضية هو 58.33.
الاستخدام والملاءمة
تعني الهارمونيك ، مثلها مثل صيغ المتوسط الأخرى ، أن لها أيضًا العديد من الاستخدامات وتستخدم بشكل أساسي في مجال التمويل لمتوسط بيانات معينة مثل مضاعفات الأسعار. يجب ألا يتم حساب متوسط المضاعفات المالية مثل نسبة السعر إلى العائد باستخدام المتوسط العادي أو المتوسط الحسابي لأن هذه المتوسطات منحازة نحو القيم الأكبر يعني التوافقية يمكن أيضًا استخدامها لتحديد نوع معين من الأنماط مثل متواليات فيبوناتشي المستخدمة بشكل رئيسي في التحليل الفني من قبل فنيي السوق.
يتعامل المتوسط التوافقي أيضًا مع متوسطات الوحدات مثل المعدلات أو النسب أو السرعة ، إلخ. أيضًا ، من المهم ملاحظة أنه يتأثر بالقيم القصوى في مجموعة البيانات المحددة أو في مجموعة معينة من الملاحظات.
يتم تعريف المتوسط التوافقي بشكل صارم ويستند إلى جميع القيم أو جميع الملاحظات في مجموعة بيانات أو عينة معينة ويمكن أن يكون مناسبًا لمزيد من المعالجة الرياضية. مثل الوسط الهندسي ، لا يتأثر المتوسط التوافقي أيضًا كثيرًا بالتقلبات في الملاحظات أو أخذ العينات. هذا من شأنه أن يعطي أهمية أكبر للقيم الصغيرة أو الملاحظات الصغيرة وهذا لن يكون مفيدًا إلا عندما تحتاج هذه القيم الصغيرة أو تلك الملاحظات الصغيرة إلى إعطاء وزن أكبر.