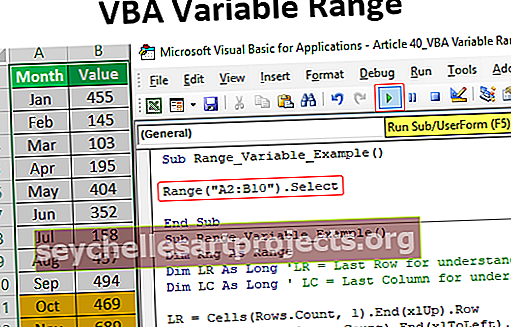
سعر الفائدة الفعلي (التعريف ، الصيغة) | كيفية حساب؟
تعريف سعر الفائدة الفعال
معدل الفائدة الفعلي ، المعروف أيضًا باسم المعدل السنوي المعادل ، هو معدل الفائدة الذي يدفعه أو يكسبه الشخص فعليًا على الأداة المالية والذي يتم حسابه من خلال مراعاة تأثير المركب على مدار الفترة الزمنية.
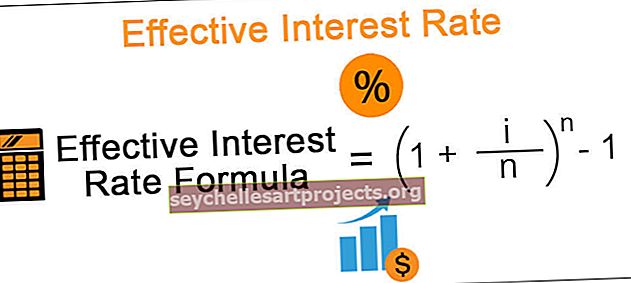
معادلة سعر الفائدة الفعالة
معادلة سعر الفائدة الفعلية = (1 + i / n) n -
هنا ، i = معدل الفائدة السنوي الذي تم ذكره في الأداة.
ن = يمثل عدد الفترات المركبة في السنة.
التفسيرات
يضاعف من معدل الفائدة. هذا هو السبب في أن معدل الفائدة المكتوب على الأداة ليس معدل فائدة فعال (معدل سنوي معادل) للمستثمر. على سبيل المثال ، إذا تمت كتابة معدل فائدة 11٪ على الأداة وتضاعف معدل الفائدة أربع مرات في السنة ، فلا يمكن أن يكون المعدل السنوي المكافئ 11٪.
ماذا سيكون بعد ذلك؟
سيكون - (1 + i / n) n - 1 = (1 + 0.11 / 4) 4-1 = 1.1123-1 = 0.1123 = 11.23٪.
هذا يعني أن 11.23٪ سيكون معدل الفائدة الفعلي للمستثمر.
حتى لو كان التغيير ضئيلًا ، فإنه يختلف عن معدل الفائدة السنوي المذكور في الأداة.
مثال
مثال 1
اشترى تينج أداة معينة. معدل الفائدة المذكور على الأداة هو 16٪. لقد استثمر حوالي 100000 دولار. يتم تجميع الأداة سنويًا. ما هو معدل الفائدة الفعلي (AER) لهذه الأداة المعينة؟ كم سيحصل كل عام كمصلحة؟
معدل الفائدة الفعلي والسعر السنوي ليسا متماثلين دائمًا لأن الفائدة تتضاعف عدة مرات كل عام. في بعض الأحيان ، يتم مضاعفة معدل الفائدة بشكل نصف سنوي أو ربع سنوي أو شهري. وهذه هي الطريقة التي يختلف بها معدل المكافئ السنوي عن معدل الفائدة السنوي.
هذا المثال يوضح لك ذلك.
دعونا نحسب.
نظرًا لأن معدل الفائدة يتراكم سنويًا ، فستكون هذه صيغة معدل الفائدة الفعلي -
(1 + i / n) n - 1 = (1 + 0.16 / 1) 1 - 1 = 1.16 - 1 = 0.16 = 16٪.
وهذا يعني في هذا المثال بالذات ، أنه لن يكون هناك فرق بين معدل الفائدة السنوي والمعدل السنوي المعادل (AER).
كل عام ستحصل Ting على فائدة = ($ 100،000 * 16٪) = $ 16،000 على الأداة.
المثال رقم 2
اشترى تونغ أداة معينة. معدل الفائدة المذكور على الأداة هو 16٪. لقد استثمر حوالي 100000 دولار. تتجمع الآلة ست مرات في السنة. ما هو المعدل السنوي المكافئ (AER) لهذه الأداة المعينة؟ كم سيحصل كل عام كمصلحة؟
هذا مجرد امتداد للمثال السابق.
لكن هناك فرق كبير.
في المثال السابق ، تم تجميع الأداة مرة واحدة في السنة مما جعل معدل الفائدة السنوي مشابهًا لمعدل المكافئ السنوي.
ومع ذلك ، في هذه الحالة ، يكون السيناريو مختلفًا تمامًا.
هنا لدينا معدل الفائدة الذي يتضاعف ست مرات في السنة.
إذن ، ها هي صيغة معدل الفائدة السنوي -
(1 + i / n) n - 1 = (1 + 0.16 / 6) 6-1 = 1.171 - 1 = 0.171 = 17.1٪.
يمكنك الآن أن ترى أنه إذا تضاعف معدل الفائدة ست مرات في السنة ، فإن المعدل السنوي المعادل يصبح مختلفًا تمامًا.
الآن ، نظرًا لأن لدينا معدل فائدة فعلي ، يمكننا حساب الفائدة التي سيحصل عليها Tong في نهاية العام.
سيحصل تونغ على = (100،000 دولار أمريكي * 17.1٪) = 17،100 دولار أمريكي.
إذا قارنا الفائدة التي يحصل عليها Ting في المثال السابق مع فائدة Tong حيث تتراكم أسعار الفائدة بشكل مختلف ، فسنرى أن هناك فرقًا في الفائدة يبلغ 1100 دولارًا تقريبًا.
المثال رقم 3
استثمر Ping في أداة. لقد استثمرت 10000 دولار. معدل الفائدة المذكور في الأداة هو 18٪. الفائدة تتضاعف شهريا. اكتشف كيف سيحصل Ping في السنة الأولى على الفائدة كل شهر.
هذا مثال مفصل للغاية عن المعدل السنوي المعادل.
في هذا المثال ، سوف نوضح كيف يتم الحساب فعليًا دون استخدام صيغة معدل الفائدة الفعلي.
لنلقي نظرة.
نظرًا لأن معدل الفائدة يتراكم شهريًا ، فإن التقسيم الفعلي لسعر الفائدة المذكور شهريًا = (18/12) = 1.5٪.
- في الشهر الأول ، سيحصل Ping على فائدة = (10،000 * 1.5٪) = $ 150.
- في الشهر الثاني ، سيتلقى Ping فائدة = {(10،000 + 150) * 1.5٪} = (10،150 * 1.5٪) = 152.25 دولارًا.
- في الشهر الثالث ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25) * 1.5٪} = (10،302.25 * 1.5٪) = 154.53 دولارًا أمريكيًا.
- في الشهر الرابع ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53) * 1.5٪} = (10،456.78 * 1.5٪) = 156.85 دولارًا أمريكيًا.
- في الشهر الخامس ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85) * 1.5٪} = (10613.63 * 1.5٪) = 159.20 دولارًا.
- في الشهر السادس ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85 + 159.20) * 1.5٪} = (10،772.83 * 1.5٪) = 161.59 دولارًا.
- في الشهر السابع ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59) * 1.5٪} = (10934.42 * 1.5٪) = 164.02 دولارًا أمريكيًا.
- في الشهر الثامن ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02) * 1.5٪} = (11098.44 * 1.5٪) = 166.48 دولارًا أمريكيًا.
- في الشهر التاسع ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48) * 1.5٪} = (11264.92 * 1.5٪) = 168.97 دولارًا.
- في الشهر العاشر ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97) * 1.5٪} = (11433.89 * 1.5٪) = 171.51 دولارًا أمريكيًا.
- في الشهر الحادي عشر ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51) * 1.5٪} = (11605.40 * 1.5٪) = 174.09 دولارًا.
- في الشهر الثاني عشر ، سيتلقى Ping فائدة = {(10،000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09) * 1.5٪} = (11779.49 * 1.5٪) = 176.69 دولارًا أمريكيًا.
إجمالي الفائدة التي حصل عليها Ping للسنة هي -
- (150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09 + 176.69) = 1956.18 دولار.
- صيغة المعدل السنوي المكافئ = (1 + i / n) n - 1 = (1 + 0.18 / 12) 12-1 = 1.195618-1 = 0.195618 = 19.5618٪.
لذلك ، فإن الفائدة التي سيحصل عليها Ping = ($ 10،000 ^ 19.5618٪) = $ 1956.18.
معدل الفائدة الفعلي في Excel
لإيجاد معدل الفائدة الفعلي أو المعدل السنوي المكافئ في Excel ، نستخدم تأثير وظيفة Excel.

- nominal_rate هو معدل الفائدة
- nper هو عدد الفترات المركبة لكل سنة
دعونا نرى المثال أدناه

- إذا كان لديك معدل فائدة رمزي قدره 10٪ مركبة سنويًا ، فإن المعدل السنوي المكافئ هو نفسه 10٪.
- إذا كان لديك معدل فائدة رمزي قدره 10٪ مركبة على ستة أشهر ، فإن المعدل السنوي المكافئ هو نفسه 10.25٪.
- إذا كان لديك معدل فائدة اسمي قدره 10٪ مركبة على أساس ربع سنوي ، فإن المعدل السنوي المكافئ هو نفسه 10.38٪.
- إذا كان لديك معدل فائدة رمزي يبلغ 10٪ مركبة شهريًا ، فإن المعدل السنوي المكافئ هو نفسه 10.47٪.
- إذا كان لديك معدل فائدة رمزي يبلغ 10٪ مركبة يوميًا ، فإن معدل الفائدة الفعلي هو نفسه 10.52٪.
قراءات المقترحة
كان هذا هو دليل سعر الفائدة الفعال وتعريفه. نناقش هنا معادلة معدل الفائدة الفعلي جنبًا إلى جنب مع العمليات الحسابية خطوة بخطوة. لمزيد من المعلومات ، يمكنك الرجوع إلى المقالات التالية
- مثال على سعر الفائدة السلبي
- احسب معدل المشاركة
- الفروق - معدل الخصم مقابل سعر الفائدة
- معادلة سعر الفائدة الاسمية
- الاندماج المشترك <