صيغة اختبار Z في الإحصاء | حساب خطوة بخطوة (أمثلة)
صيغة لحساب اختبار Z في الإحصاء
يشير اختبار Z في الإحصاء إلى اختبار الفرضية الذي يستخدم لتحديد ما إذا كانت العيّنتان الوسيتان المحسوبتان مختلفتين ، في حالة توفر الانحرافات المعيارية وكانت العينة كبيرة.
Z = (س - μ) / ơ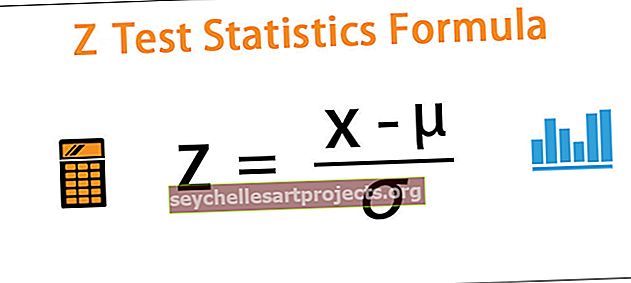
حيث x = أي قيمة من السكان
- μ = متوسط السكان
- ơ = الانحراف المعياري للسكان
في حالة العينة ، تُحسب معادلة إحصائيات اختبار z للقيمة عن طريق خصم متوسط العينة من قيمة x ثم تُقسَّم النتيجة على الانحراف المعياري للعينة. رياضيا ، يتم تمثيلها على أنها ،
Z = (x - x_mean ) / ثانيةأين
- س = أي قيمة من العينة
- x_mean = متوسط العينة
- s = عينة الانحراف المعياري
حساب اختبار Z (خطوة بخطوة)
تُشتق معادلة إحصائيات z-test لمجتمع باستخدام الخطوات التالية:
- الخطوة 1: أولاً ، احسب متوسط عدد السكان والانحراف المعياري للسكان بناءً على الملاحظة التي تم التقاطها في وسط المجتمع ، ويتم الإشارة إلى كل ملاحظة بواسطة x i . يتم الإشارة إلى العدد الإجمالي للملاحظات في السكان بواسطة N.
متوسط عدد السكان،

الانحراف المعياري السكان،

- الخطوة 2: أخيرًا ، يتم حساب إحصائيات اختبار z عن طريق خصم متوسط السكان من المتغير ثم يتم تقسيم النتيجة على الانحراف المعياري للمحتوى كما هو موضح أدناه.
Z = (س - μ) / ơ
يتم اشتقاق معادلة إحصائيات اختبار z لعينة باستخدام الخطوات التالية:
- الخطوة 1: أولاً ، احسب متوسط العينة وعينة الانحراف المعياري كما هو مذكور أعلاه. هنا ، يُشار إلى العدد الإجمالي للملاحظات في العينة بالرمز n بحيث أن n <N.
متوسط العينة ،

الانحراف المعياري للعينة،

- الخطوة 2: أخيرًا ، يتم حساب إحصائيات اختبار z عن طريق خصم متوسط العينة من قيمة x ثم يتم تقسيم النتيجة على الانحراف المعياري للعينة كما هو موضح أدناه.
Z = (x - x_mean ) / ثانية
أمثلة
يمكنك تنزيل قالب Excel لصيغة اختبار Z من هنا - نموذج Z Test Formula Excelمثال 1
لنفترض أن عددًا من الطلاب في المدرسة حضروا لاختبار الفصل. متوسط الدرجة في الاختبار هو 75 والانحراف المعياري هو 15. تحديد درجة z-test لديفيد الذي سجل 90 في الاختبار.
معطى،
- متوسط السكان ، μ = 75
- الانحراف المعياري للسكان ، ơ = 15

لذلك ، يمكن حساب إحصائيات اختبار z على النحو التالي ،

Z = (90-75) / 15
ستكون إحصائيات اختبار Z -

- Z = 1
لذلك ، فإن درجة اختبار David هي انحراف معياري واحد فوق متوسط درجات السكان ، أي وفقًا لجدول z-Score ، 84.13٪ من الطلاب أقل درجة من David.
المثال رقم 2
لنأخذ مثال 30 طالبًا تم اختيارهم كجزء من عينة فريق ليتم مسحهم لمعرفة عدد أقلام الرصاص التي تم استخدامها في الأسبوع. حدد درجة اختبار z للطالب الثالث بناءً على الإجابات المعطاة: 3 ، 2 ، 5 ، 6 ، 4 ، 7 ، 4 ، 3 ، 3 ، 8 ، 3 ، 1 ، 3 ، 6 ، 5 ، 2 ، 4 ، 3 ، 6 ، 4 ، 5 ، 2 ، 2 ، 4 ، 4 ، 2 ، 8 ، 3 ، 6 ، 7.
معطى،
- x = 5 ، منذ إجابة الطالب الثالث ، هي 5
- حجم العينة ، ن = 30
متوسط العينة ، = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30
يعني = 4.17
الآن ، يمكن حساب الانحراف المعياري للعينة باستخدام الصيغة أعلاه.
ơ = 1.90
لذلك ، يمكن حساب درجة اختبار z للطالب الثالث على النحو التالي ،
Z = (س - س) / ث
- Z = (5 –17) / 1.90
- Z = 0.44
لذلك ، فإن استخدام الطالب الثالث هو 0.44 ضعف الانحراف المعياري أعلى من متوسط استخدام العينة ، أي وفقًا لجدول z- درجة ، يستخدم 67٪ من الطلاب أقلام رصاص أقل من الطالب الثالث.
المثال رقم 3
لنأخذ مثال 30 طالبًا تم اختيارهم كجزء من عينة فريق ليتم مسحهم لمعرفة عدد أقلام الرصاص التي تم استخدامها في الأسبوع. حدد درجة اختبار z للطالب الثالث بناءً على الإجابات المعطاة: 3 ، 2 ، 5 ، 6 ، 4 ، 7 ، 4 ، 3 ، 3 ، 8 ، 3 ، 1 ، 3 ، 6 ، 5 ، 2 ، 4 ، 3 ، 6 ، 4 ، 5 ، 2 ، 2 ، 4 ، 4 ، 2 ، 8 ، 3 ، 6 ، 7.
يوجد أدناه بيانات لحساب إحصائيات اختبار Z.


يمكنك الرجوع إلى ورقة Excel المحددة أدناه للحصول على الحساب التفصيلي لإحصائيات اختبار Z.
الصلة والاستخدامات
من المهم جدًا فهم مفهوم إحصائيات اختبار z لأنه يتم استخدامه عادةً كلما كان قابلاً للجدل فيما إذا كانت إحصائية الاختبار تتبع التوزيع الطبيعي بموجب فرضية العدم المعنية أم لا. ومع ذلك ، يجب أن يوضع في الاعتبار أنه لا يتم استخدام اختبار z إلا عندما يكون حجم العينة أكبر من 30 ، وإلا فسيتم استخدام اختبار t.