انحدار المربعات الصغرى - كيفية إنشاء خط أفضل ملاءمة؟
تعريف طريقة انحدار المربعات الصغرى
طريقة انحدار المربعات الصغرى هي شكل من أشكال تحليل الانحدار الذي يؤسس العلاقة بين المتغير التابع والمستقل إلى جانب الخط الخطي. يشار إلى هذا الخط باسم "الخط الأفضل ملاءمة".
تحليل الانحدار هو طريقة إحصائية يمكن من خلالها تقدير أو توقع القيم غير المعروفة لمتغير واحد من القيم المعروفة لمتغير آخر. المتغير الذي يستخدم للتنبؤ بالفائدة المتغيرة يسمى المتغير المستقل أو التوضيحي والمتغير الذي يتم توقعه يسمى المتغير التابع أو المتغير الموضح.
دعونا نفكر في متغيرين x & y. يتم رسمها على الرسم البياني بقيم x على قيم المحور x لـ y على المحور y. يتم تمثيل هذه القيم بالنقاط في الرسم البياني أدناه. يتم رسم خط مستقيم من خلال النقاط - يشار إليها بالخط الأفضل ملاءمة.

الهدف من انحدار المربعات الصغرى هو التأكد من أن الخط المرسوم من خلال مجموعة القيم المقدمة يؤسس أقرب علاقة بين القيم.
صيغة انحدار المربعات الصغرى
يتم حساب خط الانحدار تحت طريقة المربعات الصغرى باستخدام الصيغة التالية -
ŷ = أ + ب س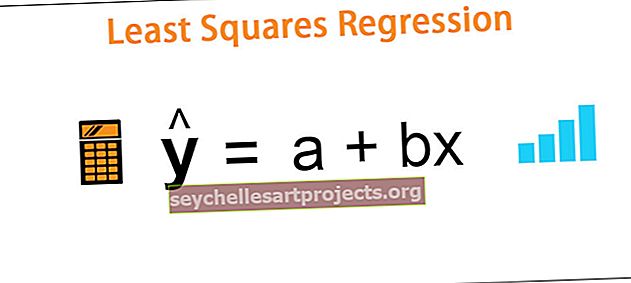
أين،
- ŷ = متغير تابع
- س = متغير مستقل
- أ = تقاطع ص
- ب = ميل الخط
يتم حساب ميل الخط ب باستخدام الصيغة التالية -

أو

تقاطع Y ، يتم حساب "a" باستخدام الصيغة التالية -

خط أفضل ملاءمة في انحدار المربع الأقل
إن أفضل خط مناسب هو خط مستقيم مرسوم من خلال مجموعة من نقاط البيانات التي تمثل العلاقة بينهما على أفضل وجه.
دعونا نفكر في الرسم البياني التالي حيث يتم رسم مجموعة من البيانات على طول المحور x و y. يتم تمثيل نقاط البيانات هذه باستخدام النقاط الزرقاء. يتم رسم ثلاثة خطوط من خلال هذه النقاط - خط أخضر وخط أحمر وخط أزرق. يمر الخط الأخضر بنقطة واحدة ويمر الخط الأحمر عبر ثلاث نقاط بيانات. ومع ذلك ، يمر الخط الأزرق من خلال أربع نقاط بيانات والمسافة بين النقاط المتبقية والخط الأزرق ضئيلة مقارنة بالخطين الآخرين.

في الرسم البياني أعلاه ، يمثل الخط الأزرق الخط الأفضل ملاءمة لأنه يقع بالقرب من جميع القيم والمسافة بين النقاط خارج الخط إلى الخط الأدنى (أي المسافة بين النقاط المتبقية إلى الخط الأفضل ملاءمة - يشار إليها أيضًا بمجموع مربعات المخلفات). في الخطين الآخرين ، البرتقالي والأخضر ، تكون المسافة بين بقايا السطور أكبر مقارنة بالخط الأزرق.
توفر طريقة المربعات الصغرى أقرب علاقة بين المتغيرات التابعة والمستقلة عن طريق تقليل المسافة بين القيم المتبقية والخط الأفضل ملاءمة ، أي أن مجموع مربعات القيم المتبقية يكون ضئيلاً في ظل هذا النهج. ومن هنا جاء مصطلح "المربعات الصغرى".
أمثلة على خط انحدار المربعات الصغرى
دعونا نطبق هذه الصيغ في السؤال أدناه -
يمكنك تنزيل قالب Excel الخاص بانحدار المربعات الصغرى من هنا - قالب Excel لانحدار المربعات الصغرىمثال 1
يتم توفير التفاصيل المتعلقة بخبرة الفنيين في شركة (في عدد من السنوات) وتقييم أدائهم في الجدول أدناه. باستخدام هذه القيم ، قم بتقدير تصنيف الأداء لفني لديه 20 عامًا من الخبرة.

المحلول -
لحساب المربعات الصغرى أولاً ، سنحسب تقاطع Y (أ) وميل الخط (ب) على النحو التالي -

منحدر الخط (ب)

- ب = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
- = 247/218
- = 1.13
تقاطع Y (أ)

- أ = 648 - (1.13) (80) / 8
- = 69.7
يتم حساب خط الانحدار على النحو التالي -

استبدال 20 بقيمة x في الصيغة ،
- ŷ = أ + ب س
- ŷ = 69.7 + (1.13) (20)
- ŷ = 92.3
يقدر تصنيف أداء فني لديه 20 عامًا من الخبرة بـ 92.3.
المثال رقم 2
معادلة انحدار المربعات الصغرى باستخدام Excel
يمكن حساب معادلة انحدار المربعات الصغرى باستخدام برنامج Excel من خلال الخطوات التالية -
- أدخل جدول البيانات في Excel.

- أدخل رسمًا بيانيًا مبعثرًا باستخدام نقاط البيانات.

- أدخل خط اتجاه داخل الرسم البياني المبعثر.

- ضمن خيارات خط الاتجاه - حدد خط الاتجاه الخطي وحدد عرض المعادلة على الرسم البياني.

- يتم عرض معادلة انحدار المربعات الصغرى لمجموعة معينة من بيانات Excel على الرسم البياني.

وبالتالي ، يتم حساب معادلة انحدار المربعات الصغرى لمجموعة معينة من بيانات Excel. باستخدام المعادلة ، يمكن إجراء تنبؤات وتحليلات للاتجاهات. توفر أدوات Excel أيضًا حسابات انحدار مفصلة.
مزايا
- طريقة المربعات الصغرى لتحليل الانحدار هي الأنسب لنماذج التنبؤ وتحليل الاتجاه. من الأفضل استخدامه في مجالات الاقتصاد والتمويل وأسواق الأوراق المالية حيث يتم التنبؤ بقيمة أي متغير مستقبلي بمساعدة المتغيرات الحالية والعلاقة بينها.
- توفر طريقة المربعات الصغرى أقرب علاقة بين المتغيرات. يكون الفرق بين مجاميع مربعات القيم المتبقية لخط أفضل ملاءمة ضئيلًا في ظل هذه الطريقة.
- آلية الحساب بسيطة وسهلة التطبيق.
سلبيات
- تعتمد طريقة المربعات الصغرى على إنشاء أقرب علاقة بين مجموعة معينة من المتغيرات. آلية الحساب حساسة للبيانات وفي حالة وجود أي قيم متطرفة (بيانات استثنائية) قد تميل النتائج إلى التأثير بشكل كبير.
- هذا النوع من الحسابات هو الأنسب للنماذج الخطية. بالنسبة للمعادلات غير الخطية ، يتم تطبيق آليات حسابية أكثر شمولاً.
استنتاج
طريقة المربعات الصغرى هي إحدى الطرق الأكثر استخدامًا لنماذج التنبؤ وتحليل الاتجاه. عند حسابها بشكل مناسب ، فإنها تحقق أفضل النتائج.