seychellesartprojects.org

العائد المعدل حسب المخاطر هو أسلوب لقياس وتحليل عوائد الاستثمار الذي يتم فيه تحليل المخاطر المالية والسوقية والائتمانية والتشغيلية وتعديلها بحيث يمكن للفرد اتخاذ قرار بشأن ما إذا كان الاستثمار يستحق ذلك مع جميع المخاطر. يطرح على رأس المال المستثمر.

لماذا نستثمر في المال؟ بسيط. لجني العوائد. لكن هل فكرنا يومًا ما إذا كان العائد مبررًا بما يكفي لعوامل الخطر الكامنة؟ في حين أن الناس عادة ما يكون لديهم هذا التصور حول العوائد التي تدر المال ، فإن المخاطرة هي عنصر ينسى كثيرًا. العوائد ليست سوى المكاسب من الفائض المستثمر: الأموال التفاضلية المكتسبة. من الناحية الاقتصادية البحتة ، إنها طريقة للنظر في الأرباح فيما يتعلق برأس المال المستثمر.

في هذه المقالة ، نناقش العوائد المعدلة حسب المخاطر بالتفصيل -

كيف يتم تعريف المخاطر؟

التعريف القياسي لمخاطر الاستثمار هو انحراف عن النتيجة المتوقعة . يمكن التعبير عنها بعبارات مطلقة أو فيما يتعلق بشيء مثل معيار السوق. يمكن أن يكون هذا الانحراف موجبًا أو سلبيًا. إذا كان المستثمر يخطط لتحقيق عوائد أعلى ، على المدى الطويل ، يجب أن يكون أكثر انفتاحًا على التقلبات قصيرة الأجل. يعتمد مقدار التقلب على تحمل المخاطر للمستثمر. تحمل المخاطر ليس سوى الميل لتحمل التقلبات لظروف مالية محددة ، مع الأخذ في الاعتبار السهولة النفسية النفسية مع عدم اليقين واحتمال تكبد خسائر كبيرة على المدى القصير.

العوائد المعدلة حسب المخاطر وأهميتها

يعمل العائد المعدل حسب المخاطر على ضبط عائد الاستثمار من خلال قياس مقدار المخاطر التي ينطوي عليها إنتاج هذا العائد. المحافظ الاستثمارية المكونة من صفقات الأسهم والصناديق المشتركة وصناديق الاستثمار المتداولة. يتم استخدام مفهوم العائد المعدل حسب المخاطر لمقارنة عوائد المحافظ مع مستويات مخاطر مختلفة مقابل معيار مع بيان عائد ومخاطر معروف.

إذا كان للأصل حاصل مخاطرة أقل من السوق ، فإن عائد الأصل فوق المعدل الخالي من المخاطر يعتبر مكسبًا كبيرًا. إذا كان الأصل يمثل مستوى أعلى من مستوى مخاطر السوق ، يتم تقليل العائد التفاضلي الخالي من المخاطر.

تعتبر العوائد المعدلة حسب المخاطر أمرًا بالغ الأهمية لأنها تساعد في حل ثلاث مشكلات رئيسية:

هناك 6 طرق شائعة الاستخدام لحساب العائد المعدل حسب المخاطر. ننظر إليهم بالتفصيل أدناه -

# 1 - نسبة شارب (العائد المعدل حسب المخاطر)

يرمز معنى نسبة شارب إلى أي مدى يعوض عائد الأصل المستثمر عن المخاطرة التي يتعرض لها. عند مقارنة أصلين بمعيار مشترك ، فإن الأصل الذي يحتوي على نسبة شارب أعلى يوفر عائدًا أفضل لنفس المخاطر (أو ، على نحو مكافئ ، نفس العائد لمخاطر أقل). طورها الفائز بجائزة نوبل ، ويليام ف. شارب في عام 1966 ، يتم تعريف نسبة شارب على أنها متوسط ​​العائد المكتسب الذي يزيد عن المعدل الخالي من المخاطر لكل وحدة تقلب أو إجمالي المخاطر ، أي الانحراف المعياري. أصبحت نسبة شارب الطريقة الأكثر استخدامًا لحساب العائد المعدل حسب المخاطر ، ومع ذلك ، لا يمكن أن تكون دقيقة إلا إذا كانت البيانات لها توزيع طبيعي.

• Rp = عائد المحفظة المتوقع
• Rf - معدل الخالي من المخاطر
• سيجما (ع) = الانحراف المعياري للمحفظة

يمكن أن تساعد نسبة شارب أيضًا في تحديد ما إذا كانت العوائد الزائدة للأوراق المالية ناتجة عن قرارات استثمارية حكيمة أو مجرد مخاطر كبيرة. حتى مع وجود صندوق أو ورقة مالية واحدة يمكن أن تجني عوائد أعلى من نظيراتها ، يمكن اعتبار الاستثمار جيدًا إذا كانت تلك العوائد الأعلى خالية من عنصر المخاطرة الإضافية. كلما زادت نسبة شارب ، كان أداءها المعدل حسب المخاطر أفضل.

مثال على نسبة شارب

لنفترض أن العائد السنوي لمدة 10 سنوات لمؤشر S&P 500 (محفظة السوق) هو 10٪ ، في حين أن متوسط ​​العائد السنوي على أذون الخزانة (وكيل جيد للمعدل الخالي من المخاطر) هو 5٪. الانحراف المعياري هو 15٪ خلال فترة 10 سنوات.

المديرين	متوسط ​​العائد السنوي	الانحراف المعياري للمحفظة	رتبة
الصندوق أ	10٪	0.95	ثالثا
الصندوق ب	12٪	0.30	أنا
الصندوق ج	8٪	0.28	ثانيًا

• السوق = (.10-.05) /0.15 = 0.33
• (الصندوق أ) = (0.10-.05) /0.95 = 0.052
• (الصندوق ب) = (0.12-.05) /0.30 = 0.233
• (الصندوق ج) = (.08-.05) /0.28 = .0.107

# 2 - نسبة ترينور (العائد المعدل حسب المخاطر)

Treynor هو قياس للعائدات المكتسبة التي تزيد عن تلك التي كان يمكن جنيها من استثمار ليس له مخاطر متنوعة. باختصار ، إنها أيضًا نسبة تقلب المكافأة ، تمامًا مثل نسبة شارب ، ولكن بفارق واحد فقط. يستخدم معامل بيتا بدلاً من الانحرافات المعيارية.

• Rp = عائد المحفظة المتوقع
• Rf - معدل الخالي من المخاطر
• بيتا (ع) = محفظة بيتا

تحدد هذه النسبة التي طورها Jack L. Treynor مدى نجاح الاستثمار في توفير تعويض للمستثمرين ، مع مراعاة مستوى المخاطرة الكامن في الاستثمار. تعتمد نسبة ترينور على بيتا - الذي يصور حساسية الاستثمار للحركات في السوق - لتقييم المخاطر. تستند نسبة Treynor على فرضية أن المخاطرة بعنصر متكامل في السوق بالكامل (كما هو موضح في الإصدار التجريبي) يجب تغريمه لأن التنويع لا يمكن القضاء عليه.

عندما تكون قيمة نسبة Treynor عالية ، فهذه علامة على أن المستثمر قد حقق عوائد عالية على كل من مخاطر السوق التي افترضها. تساعد نسبة Treynor الشخص على فهم كيفية أداء كل استثمار ضمن المحفظة. بهذه الطريقة ، يكتسب المستثمر أيضًا فكرة عن مدى كفاءة استخدام رأس المال.

تحقق أيضًا من CAPM Beta

مثال على نسبة ترينور

لنفترض أن العائد السنوي لمدة 10 سنوات لمؤشر S&P 500 (محفظة السوق) هو 10٪ ، في حين أن متوسط ​​العائد السنوي على أذون الخزانة (وكيل جيد للمعدل الخالي من المخاطر) هو 5٪.

المديرين	متوسط ​​العائد السنوي	بيتا	رتبة
الصندوق أ	12٪	0.95	ثانيًا
الصندوق ب	15٪	1.05	أنا
الصندوق ج	10٪	1.10	ثالثا

• السوق = (.10-.05) / 1 = .05
• (الصندوق أ) = (.12-.05) / 0.95 = .073
• (الصندوق ب) = (.15-.05) /1.05 = .095.00
• (الصندوق ج) = (.10-.05) /1.10 = .045

# 3 - ألفا جنسن (العائد المعدل حسب المخاطر)

غالبًا ما يعتبر Alpha عائدًا نشطًا على الاستثمار. يحدد أداء الاستثمار مقابل مؤشر السوق المستخدم كمعيار ، حيث يُنظر إليه غالبًا على أنه يمثل حركة السوق ككل. العوائد الزائدة للصندوق مقارنة بعائد المؤشر القياسي هي ألفا للصندوق. في الأساس ، يشير معامل ألفا إلى كيفية أداء الاستثمار بعد احتساب المخاطر التي ينطوي عليها:

• Rp = عائد المحفظة المتوقع
• Rf - معدل الخالي من المخاطر
• بيتا (ع) = محفظة بيتا
• Rm = عائد السوق

ألفا <0: حقق الاستثمار القليل جدًا من المخاطر (أو كان محفوفًا بالمخاطر بالنسبة للعائد)

ألفا = 0: حقق الاستثمار عائدًا مناسبًا للمخاطرة التي تم التعرض لها

ألفا> 0: الاستثمار له عائد يزيد على عائد المخاطرة المفترضة

مثال ألفا لجنسن

لنفترض أن محفظة حققت عائدًا بنسبة 17٪ في العام السابق. عاد مؤشر السوق التقريبي لهذا الصندوق بنسبة 12.5٪. بيتا للصندوق مقابل نفس المؤشر هو 1.4 والمعدل الخالي من المخاطر هو 4 ٪.

وهكذا ، فإن ألفا جنسن = 17 - [4 + 1.4 * (12.5-4)]

= 17 - [4 + 1.4 * 8.5] = = 17 - [4 + 11.9]

= 1.1٪

بالنظر إلى بيتا 1.4 ، من المتوقع أن يكون الصندوق محفوفًا بالمخاطر مقارنة بمؤشر السوق وبالتالي يكسب المزيد. تعد علامة ألفا الإيجابية مؤشراً على أن مدير المحفظة قد حصل على عوائد كبيرة ليتم تعويضها عن المخاطر الإضافية التي تم التعرض لها على مدار العام. إذا كان الصندوق سيعود بنسبة 15٪ ، فإن ألفا المحسوبة ستكون -0.9٪. تشير الألفا السالبة إلى أن المستثمر لم يكن يكسب عوائد كافية مقابل مقدار المخاطرة الذي تم تحمله.

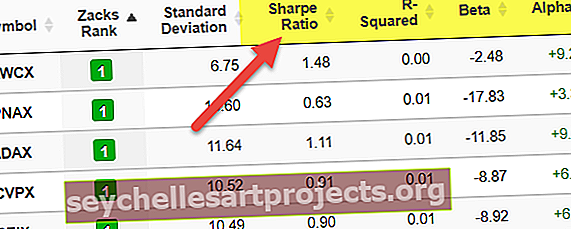
# 4 - R-Squared (العائد المعدل حسب المخاطر)

R-squared هو مقياس إحصائي يمثل النسبة المئوية لحركة الأموال أو الأوراق المالية التي تستند إلى الحركات في مؤشر مرجعي.

• تتراوح قيم R التربيعية من 0 إلى 1 وعادة ما يتم ذكرها كنسب مئوية من 0 إلى 100٪.
• إن تربيع R بنسبة 100٪ يعني أنه يمكن تبرير جميع تحركات الأمان تمامًا من خلال الحركات في المؤشر.
• يشير مربع R المرتفع ، بين 85٪ و 100٪ ، إلى أن أنماط أداء الصندوق تعكس أداء المؤشر.

ومع ذلك ، فإن الأداء القوي إلى جانب نسبة R-Squared منخفضة للغاية يعني أن هناك حاجة إلى مزيد من التحليل لتحديد سبب الأداء المتفوق.

# 5 - نسبة سورتينو (العائد المعدل حسب المخاطر)

نسبة سورتينو هي اختلاف في نسبة شارب. يأخذ سورتينو عائد المحفظة ويقسم ذلك على "مخاطر الجانب السلبي" للمحفظة. إن مخاطر الجانب السلبي هي تقلب العوائد دون مستوى محدد ، وعادة ما يكون متوسط ​​عائد المحفظة أو عوائدها أقل من الصفر. يظهر سورتينو نسبة العائد الناتج "لكل وحدة من مخاطر الهبوط".

يشمل الانحراف المعياري كلا من التقلبات الصاعدة والهابطة. ومع ذلك ، فإن معظم المستثمرين قلقون بشكل أساسي من التقلبات الهبوطية. لذلك ، فإن نسبة سورتينو تصور مقياسًا أكثر واقعية لمخاطر الهبوط المتضمنة في الصندوق أو السهم.

• Rp = عائد المحفظة المتوقع
• Rf - معدل خالي من المخاطر
• سيجما (د) = الانحراف المعياري لعوائد الأصول السلبية

مثال نسبة سورتينو

لنفترض أن الصندوق المشترك A لديه عائد سنوي قدره 15٪ وانحرافًا سلبيًا قدره 8٪. الصندوق التعاضدي ب لديه عائد سنوي قدره 12٪ وانحراف سلبي بنسبة 5٪. معدل الخالي من المخاطر 2.5٪.

سيتم حساب نسب سورتينو لكلا الصندوقين على النحو التالي:

• صندوق الاستثمار X سورتينو = (15٪ - 2.5٪) / 8٪ = 1.56
• الصندوق التعاوني Z سورتينو = (12٪ - 2.5٪) / 5٪ = 1.18

# 6 - أداء Modigliani المعدل حسب المخاطر

يُعرف أيضًا باسم مقياس Modigliani-Modigliani أو M2 ، ويتم استخدامه للوصول إلى العائد المعدل حسب المخاطر لمحفظة الاستثمار. يتم استخدامه لقياس العائد من محفظة معدلة لمخاطر الصندوق / المحفظة بالنسبة لمعيار (مثل سوق أو مؤشر معين). لقد أخذ نصيبه من الإلهام من نسبة Sharpe المقبولة على نطاق واسع ، ومع ذلك ، فإنه يتمتع بميزة كبيرة تتمثل في كونه في وحدات عائد النسبة المئوية ، مما يسهل تفسيره.

M2 = R _p  - R _m

• Rp هو العائد على المحفظة المعدلة
• Rm هو العائد على محفظة السوق

المحفظة المعدلة هي المحفظة الخاضعة للإدارة ليتم تعديلها بحيث تنطوي على مخاطر إجمالية فيما يتعلق بمحفظة السوق. يتم إنشاء المحفظة المعدلة كمجموعة من المحفظة المدارة والأصول الخالية من المخاطر حيث يتم تعيين الأوزان وفقًا للمخاطر التي تتحملها.

يمكن أن تؤدي نسبة شارب إلى تفسير مضلل عندما تكون سلبية ويصعب أيضًا مقارنة نسبة شارب بشكل مباشر في العديد من الأدوات. على سبيل المثال ، إذا كانت لدينا نسبة شارب 0.50٪ ومحفظة أخرى بنسبة -0.50٪ ، فقد لا تكون المقارنة منطقية بين المحفظتين. من السهل التعرف على حجم الاختلاف بين المحافظ الاستثمارية التي تبلغ قيم M2 5.2٪ و 5.8٪. الفرق البالغ 0.6٪ هو العائد المعدل حسب المخاطر للسنة مع تعديل المخاطرة لتلائم تلك الخاصة بالمحفظة المعيارية.

العوائد المعدلة حسب المخاطر - نسبة شارب مقابل نسبة ترينور مقابل ألفا جنسن

يتم استخدام نسبة ترينور ، مثل نسبة شارب ، بشكل أكثر فاعلية كأداة تصنيف وليس على أساس فردي. يمكن للمستثمرين مقارنة الصناديق أو محافظ الصناديق بمقادير مختلفة من مخاطر السوق لتحديد ترتيبهم وفقًا للعائد المعدل حسب المخاطر. تكون النسبة مفيدة بشكل خاص عندما يتم قياس المحافظ أو الصناديق التي تتم مقارنتها بنفس مؤشر السوق أو عند مقارنة الصندوق بمؤشره المعياري.

بالمقارنة مع نسبة شارب ، فإن قيمة نسبة ترينور نسبية: الأعلى هو الأفضل. من ناحية أخرى ، لا يمكن استخدام ألفا لجنسن إلا في سياق مطلق. تعكس علامة ألفا وحجمها مهارات مدير الصندوق وخبراته. ومع ذلك ، لكي يكون أي مقياس فعالاً ، يجب اختيار المؤشر المعياري بشكل مناسب للمحفظة قيد الدراسة.

في كثير من الأحيان ، قد يظهر المدير خبيرًا على أساس مبدأ المكافأة إلى المخاطر المنهجية ولكنه غير ماهر على أساس المكافأة إلى إجمالي المخاطر. يجب على المستثمر الذي يقارن نسبة ترينور ونسبة شارب للصندوق أن يفهم أن الاختلاف الكبير بين الاثنين يمكن أن يكون مؤشراً في الواقع على محفظة ذات نسبة كبيرة من المخاطر المميزة فيما يتعلق بالمخاطر الإجمالية. من ناحية أخرى ، سيتم تصنيف محفظة متنوعة بالكامل بشكل متماثل وفقًا للنسبتين.

ألفا جنسن

المديرين	متوسط ​​العائد السنوي	بيتا	رتبة
الصندوق أ	12٪	0.95	ثانيًا
الصندوق ب	15٪	1.05	أنا
الصندوق ج	10٪	1.10	ثالثا

أولاً ، نحسب العائد المتوقع للمحفظة:

• ER (A) = 0.05 + 0.95 * (0.1-0.05) = 0.0975 أو 9.75٪
• ER (B) = 0.05 + 1.05 * (0.1-0.05) = 0.1030 أو 10.30٪ عائد
• ER (C) == 0.05 + 1.1 * (0.1-0.05) = 0.1050 أو 10.50٪ عائد

بعد ذلك ، نحسب ألفا للمحفظة بطرح العائد المتوقع للمحفظة من العائد الفعلي:

• ألفا أ = 12٪ - 9.75٪ = 2.25٪
• ألفا ب = 15٪ - 10.30٪ = 4.70٪
• ألفا ج = 10٪ - 10.50٪ = -0.50٪

استنتاج

يتم استخدام العائد المعدل حسب المخاطر لقياس مقدار العائد الذي تحققه محفظة الاستثمار مقارنة بالمخاطر التي تنطوي عليها ، والتي يتم التعبير عنها بشكل عام كرقم ويمكن تطبيق نفس الشيء على صناديق الاستثمار والأوراق المالية الفردية والمحافظ الاستثمارية ، إلخ.

يختلف العائد المعدل حسب المخاطر من شخص لآخر ويعتمد على عدد كبير من العوامل مثل تحمل المخاطر ، وتوافر الأموال ، والاستعداد لشغل مركز لفترة طويلة لاستعادة السوق. في حالة ارتكاب المستثمر لخطأ في الحكم ، سيتم أيضًا التأكد من تكلفة الفرصة البديلة للمستثمرين وحالته الضريبية.

هناك طرق مختلفة يمكن للمستثمر من خلالها تحسين عائده المعدل حسب المخاطر. تتمثل إحدى الطرق الأكثر شيوعًا في تعديل وضع سهمه وفقًا لتقلبات السوق. عادة ما تؤدي زيادة التقلبات إلى انخفاض مركز الأسهم أو العكس. يتبنى مديرو الصناديق هذه الاستراتيجية بشكل متزايد لتفادي الخسائر الكبيرة وللتأكيد على تعظيم المكاسب.

ومع ذلك ، فإن هذه التدابير لا تحسب العائد المعدل حسب المخاطر على أساس الوقت الحقيقي. تميل معظم هذه النسب إلى استخدام المخاطر التاريخية في الحساب. هذه إحدى الثغرات الأساسية التي يشير إليها معظم الخبراء. في الحياة الواقعية ، يمكن أن يكون هناك العديد من المخاطر الكامنة وغير الملحوظة التي يمكن أن تغير ترتيب الاستثمارات. لا يمكن للمرء أبدًا حساب العائد الدقيق المعدل حسب المخاطر بسبب عدم وجود قواعد محددة. تتمثل الظاهرة الأساسية لاستخدام معدل العائد المعدل حسب المخاطر في أن المستثمر يمكنه بشكل أساسي ترتيبها من الأدنى إلى الأعلى من حيث الجاذبية.