نموذج لصيغة الانحراف المعياري | كيفية حساب؟
صيغة لحساب نموذج الانحراف المعياري
يشير الانحراف المعياري النموذجي إلى المقياس الإحصائي المستخدم لقياس مدى انحراف متغير عشوائي عن متوسط العينة ويتم حسابه عن طريق إضافة مربعات انحراف كل متغير عن المتوسط ، ثم قسمة النتيجة على عدد من المتغيرات مطروحًا منها ثم حساب الجذر التربيعي في التفوق على النتيجة.
رياضيا ، يتم تمثيلها على أنها ،
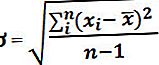
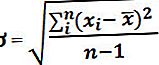
أين
- x i = ith متغير عشوائي
- X = متوسط العينة
- ن = عدد المتغيرات في العينة
حساب نموذج الانحراف المعياري (خطوة بخطوة)
- الخطوة 1: أولاً ، اجمع المتغيرات العشوائية من عدد كبير من المتغيرات. هذه المتغيرات سوف تشكل عينة. يتم الإشارة إلى المتغيرات بالرمز x i .
- الخطوة 2: بعد ذلك ، حدد عدد المتغيرات في العينة ويشار إليها بالرمز n.
- الخطوة 3: بعد ذلك ، حدد متوسط العينة عن طريق إضافة جميع المتغيرات العشوائية وقسمة النتيجة على عدد المتغيرات في العينة. يتم الإشارة إلى متوسط العينة بالرمز x.

- الخطوة 4: بعد ذلك ، احسب الفرق بين كل متغير في العينة ومتوسط العينة ، أي x i - x.
- الخطوة 5: بعد ذلك ، احسب مربع جميع الانحرافات مثل (x i - x) 2.
- الخطوة 6: بعد ذلك ، أضف كل الانحرافات التربيعية مثل ∑ (x i - x) 2.
- الخطوة 7: بعد ذلك ، قسّم مجموع كل الانحرافات التربيعية على عدد المتغيرات في العينة ناقص واحد أي (n - 1).
- الخطوة 8: أخيرًا ، تُحسب صيغة الانحراف المعياري النموذجي عن طريق حساب الجذر التربيعي للنتيجة المذكورة أعلاه كما هو موضح أدناه.

أمثلة
يمكنك تنزيل نموذج Excel لصيغة الانحراف المعياري من هنا - نموذج لصيغة Excel لصيغة الانحراف المعياريمثال 1
دعونا نأخذ مثالاً لعينة من 5 طلاب تم مسحهم لمعرفة عدد أقلام الرصاص التي كانوا يستخدمونها كل أسبوع. احسب الانحراف المعياري للعينة بناءً على إجاباتهم المعطاة: 3 ، 2 ، 5 ، 6 ، 4
معطى،
- حجم العينة (ن) = 5
فيما يلي بيانات لحساب الانحراف المعياري للعينة.

متوسط العينة
حساب متوسط العينة
متوسط العينة = (3 + 2 + 5 + 6 + 4) / 5

متوسط العينة = 4
يمكن حساب مربعات الانحرافات لكل متغير على النحو التالي ،
- (3-4) 2 = 1
- (2-4) 2 = 4
- (5-4) 2 = 1
- (6-4) 2 = 4
- (4 - 4) 2 = 0
الآن ، يمكن حساب الانحراف المعياري للعينة باستخدام الصيغة أعلاه ،
- ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 - 1)}

سيكون الانحراف -

- ơ = 1.58
لذلك ، فإن الانحراف المعياري للعينة هو 1.58.
المثال رقم 2
دعونا نأخذ على سبيل المثال مكتب في نيويورك حيث يعمل حوالي 5000 شخص وتم إجراء مسح على عينة من 10 أشخاص لتحديد متوسط عمر السكان العاملين. حدد نموذج الانحراف المعياري بناءً على أعمار الأشخاص العشرة المعطاة: 23 ، 27 ، 33 ، 28 ، 21 ، 24 ، 36 ، 32 ، 29 ، 25
معطى،
- حجم العينة (ن) = 10

باستخدام البيانات أعلاه ، سنحسب أولاً متوسط العينة
متوسط العينة
حساب متوسط العينة
= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

متوسط العينة = 27.8
يمكن حساب مربعات الانحرافات لكل متغير على النحو التالي ،
- (23 - 27.8) 2 = 23.04
- (27 - 27.8) 2 = 0.64
- (33 - 27.8) 2 = 27.04
- (28 - 27.8) 2 = 0.04
- (21 - 27.8) 2 = 46.24
- (24 - 27.8) 2 = 14.44
- (36 - 27.8) 2 = 67.24
- (32 - 27.8) 2 = 17.64
- (29 - 27.8) 2 = 1.44
- (25 - 27.8) 2 = 7.84
انحراف
الآن ، يمكن حساب الانحراف باستخدام الصيغة أعلاه ،
- ơ = √ {(23.04 + 0.64 + 27.04 + 0.04 + 46.24 +14.44 +67.24 + 17.64 + 1.44 + 7.84) / (10 - 1)}

سيكون الانحراف -

- ơ = 4.78
يمكنك الرجوع إلى ورقة Excel المقدمة أعلاه لفهم الحساب التفصيلي.
الصلة والاستخدامات
يعتبر مفهوم الانحراف المعياري للعينة مهمًا جدًا من منظور الإحصائي لأنه عادةً ما يتم أخذ عينة من البيانات من مجموعة من المتغيرات الكبيرة (السكان) التي يُتوقع من الإحصائي تقدير النتائج أو تعميمها على المجتمع بأكمله. مقياس الانحراف المعياري ليس استثناءً من ذلك ، وبالتالي ، يجب على الإحصائي إجراء تقييم للانحراف المعياري للسكان على أساس العينة المرسومة ، وهنا يأتي دور هذا الانحراف.