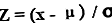صيغة نقاط Z | خطوة بخطوة حساب Z-Score
صيغة لحساب Z-Score
تشير درجة Z من البيانات الأولية إلى الدرجة الناتجة عن قياس عدد الانحرافات المعيارية أعلى أو أقل من متوسط المحتوى في البيانات ، مما يساعد في اختبار الفرضية قيد الدراسة. بمعنى آخر ، إنها مسافة نقطة البيانات من وسط المحتوى التي يتم التعبير عنها كمضاعف الانحراف المعياري.
- تختلف درجات z في نطاق -3 أضعاف الانحراف المعياري (أقصى يسار التوزيع الطبيعي) إلى +3 مرات الانحراف المعياري (أقصى يمين التوزيع الطبيعي).
- تحتوي الدرجات z على متوسط 0 وانحراف معياري قدره 1.
تُحسب معادلة z-Score لنقطة بيانات بطرح متوسط المحتوى من نقطة البيانات (المشار إليها بـ x ) ثم تُقسَّم النتيجة على الانحراف المعياري للمحتوى. رياضيا ، يتم تمثيلها على أنها ،
درجة Z = (x - μ) / ơ
أين
- س = نقطة البيانات
- μ = متوسط
- ơ = الانحراف المعياري
حساب Z Score (خطوة بخطوة)
يمكن اشتقاق معادلة z-Score لنقطة بيانات باتباع الخطوات التالية:
- الخطوة 1: أولاً ، حدد متوسط مجموعة البيانات بناءً على نقاط البيانات أو الملاحظات التي يُشار إليها بالرمز x i ، بينما يُشار إلى العدد الإجمالي لنقاط البيانات في مجموعة البيانات بالرمز N.

- الخطوة 2: بعد ذلك ، حدد الانحراف المعياري للسكان على أساس متوسط السكان μ ونقاط البيانات x i وعدد نقاط البيانات في المجموعة N.

- الخطوة 3: أخيرًا ، يتم اشتقاق z-score بطرح المتوسط من نقطة البيانات ثم يتم تقسيم النتيجة على الانحراف المعياري كما هو موضح أدناه.
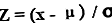
أمثلة
يمكنك تنزيل قالب Excel الخاص بصيغة Z Score من هنا - نموذج Z Score Formula Excelمثال 1
لنأخذ مثال فصل مكون من 50 طالبًا كتبوا اختبار العلوم الأسبوع الماضي. اليوم هو يوم النتيجة وقد أخبر مدرس الفصل أن جون سجل 93 في الاختبار بينما كان متوسط درجات الفصل 68. حدد درجة z لعلامة اختبار جون إذا كان الانحراف المعياري هو 13.
المحلول:
معطى،
- درجة اختبار جون ، س = 93
- يعني ، μ = 68
- الانحراف المعياري ơ = 13

لذلك ، يمكن حساب الدرجة المعيارية لدرجة اختبار جون باستخدام الصيغة أعلاه ،

Z = (93-68) / 13
ستكون نقاط Z -

درجة Z = 1.92
لذلك ، فإن درجة Ztest لجون هي 1.92 انحراف معياري أعلى من متوسط درجات الفصل ، مما يعني أن 97.26٪ من الفصل (49 طالبًا) سجلوا درجات أقل من جون.
المثال رقم 2
دعونا نأخذ مثالاً مفصلاً آخر لـ 30 طالبًا (حيث أن z-test ليس مناسبًا لأقل من 30 نقطة بيانات) الذين ظهروا في اختبار الفصل. حدد درجة اختبار z للطالب الرابع بناءً على العلامات التي سجلها الطلاب من 100-55 ، 67 ، 84 ، 65 ، 59 ، 68 ، 77 ، 95 ، 88 ، 78 ، 53 ، 81 ، 73 ، 66 ، 65 ، 52 ، 54 ، 83 ، 86 ، 94 ، 85 ، 72 ، 62 ، 64 ، 74 ، 82 ، 58 ، 57 ، 51 ، 91.
المحلول:
معطى،
- س = 65 ،
- معدل الطالب الرابع = 65 ،
- عدد نقاط البيانات ، N = 30.
المتوسط = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30
يعني = 71.30
الآن ، يمكن حساب الانحراف المعياري باستخدام الصيغة كما هو موضح أدناه ،

ơ = 13.44
لذلك ، يمكن حساب الدرجة Z للطالب الرابع باستخدام الصيغة أعلاه ،
Z = (س - س) / ث
- Z = (65 –30) / 13.44
- ض = -0.47
وبالتالي ، فإن درجة الطالب الرابع هي 0.47 انحراف معياري أقل من متوسط درجات الفصل ، مما يعني أن 31.92٪ من الفصل (10 طلاب) سجلوا درجات أقل من الطالب الرابع وفقًا لجدول z- درجة.
نقاط Z في Excel (مع قالب Excel)
الآن ، دعنا نأخذ الحالة المذكورة في المثال 2 لتوضيح مفهوم z-Score في نموذج Excel أدناه.
يوجد أدناه بيانات لحساب Z Score


يمكنك الرجوع إلى ورقة Excel المحددة أدناه للحصول على الحساب التفصيلي لإحصائيات اختبار صيغة Z للنتيجة.
الصلة والاستخدامات
من منظور اختبار الفرضيات ، تعتبر z-score مفهومًا مهمًا للغاية لفهمه لأنه يتم استخدامه لاختبار ما إذا كانت إحصائية الاختبار تقع في النطاق المقبول للقيمة أم لا. تُستخدم الدرجة المعيارية أيضًا لتوحيد البيانات قبل التحليل ، وحساب احتمال الحصول على درجة أو مقارنة نقطتين أو أكثر من نقاط البيانات التي تكون من توزيعات عادية مختلفة. هناك تطبيق متنوع لدرجة z عبر الحقول إذا تم تطبيقها بشكل صحيح.