الانحراف المعياري النسبي (التعريف ، الصيغة) | كيفية حساب؟
ما هو الانحراف المعياري النسبي؟
الانحراف المعياري النسبي (RSD) هو مقياس الانحراف لمجموعة من الأرقام المنتشرة حول المتوسط ويتم حسابه على أنه نسبة الانحراف المعياري إلى المتوسط لمجموعة من الأرقام. كلما زاد الانحراف ، زادت الأرقام عن المتوسط. خفض الانحراف ، أقرب الأرقام من المتوسط.
صيغة الانحراف المعياري النسبي
الانحراف المعياري النسبي = (الانحراف المعياري / المتوسط) * 100
الانحراف المعياري σ = √ [Σ (x- μ) 2 / N]
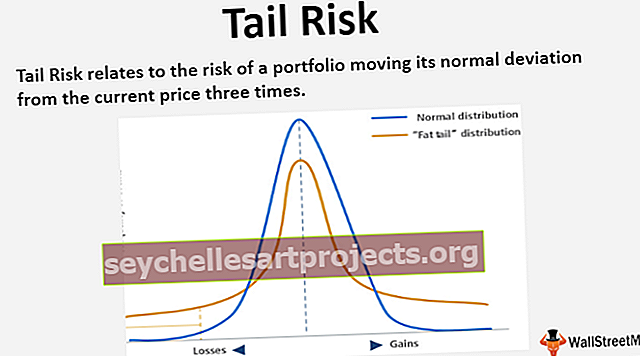
لإعطاء مثال ، في الأسواق المالية ، تساعد هذه النسبة في قياس التقلبات. تساعد صيغة تحديد وضع اللاجئ على تقييم المخاطر التي ينطوي عليها الأمن فيما يتعلق بالحركة في السوق. إذا كانت نسبة الأمان مرتفعة ، فستنتشر الأسعار وسيكون النطاق السعري واسعًا. هذا يعني أن تقلبات الأمان عالية. إذا كانت نسبة الأمان منخفضة ، فستكون الأسعار أقل تشتتًا. هذا يعني أن تقلبات الأمان منخفضة.
كيف تحسب الانحراف المعياري النسبي؟ (خطوة بخطوة)
- الخطوة 1: أولاً ، احسب المتوسط (μ) أي متوسط الأرقام
- الخطوة 2: بمجرد أن نحصل على المتوسط ، اطرح المتوسط من كل رقم مما يعطينا الانحراف ، تربيع الانحرافات.
- الخطوة 3: اجمع الانحرافات التربيعية واقسم هذه القيمة على العدد الإجمالي للقيم. هذا هو التباين.
- الخطوة 4: الجذر التربيعي للتباين سيعطينا الانحراف المعياري (σ).
- الخطوة 5: قسّم الانحراف المعياري على المتوسط واضرب هذا في 100
- الخطوة 6: يا هلا! لقد انتهيت للتو من كيفية حساب صيغة الانحراف المعياري النسبي
للتلخيص ، بقسمة الانحراف المعياري مع المتوسط والضرب في 100 يعطي الانحراف المعياري النسبي. هذا هو مدى بساطة!
قبل أن نمضي قدمًا ، هناك بعض المعلومات التي يجب أن تعرفها. عندما تكون البيانات عبارة عن مجتمع بمفردها ، تكون الصيغة المذكورة أعلاه مثالية ولكن إذا كانت البيانات عينة من مجتمع (على سبيل المثال ، وحدات بت وأجزاء من مجموعة أكبر) ، فسيتغير الحساب.
التغيير في الصيغة على النحو التالي:
الانحراف المعياري (نموذج) σ = [Σ (x- μ) 2 / N-1]
عندما تكون البيانات عبارة عن مجموعة سكانية ، يجب تقسيمها على N.
عندما تكون البيانات عينة ، يجب تقسيمها على N-1.
أمثلة
يمكنك تنزيل نموذج Excel لصيغة الانحراف المعياري النسبي هنا - نموذج Excel لصيغة الانحراف المعياري النسبيمثال 1
العلامات التي حصل عليها 3 طلاب في الاختبار هي كالتالي: 98 و 64 و 72. احسب الانحراف المعياري النسبي؟
المحلول:
فيما يلي بيانات للحساب

يعني
حساب المتوسط

μ = Σx / ن
أين μ هو المتوسط ؛ Σxi هو مجموع كل القيم و n هو عدد العناصر
μ = (98 + 64 + 72) / 3
μ = 78
الانحراف المعياري
لذلك ، يكون حساب الانحراف المعياري على النحو التالي ،

بجمع قيم كل (x- μ) 2 نحصل على 632
لذلك ، Σ (x- μ) 2 = 632
حساب الانحراف المعياري:
σ = √ [Σ (x- μ) 2 / N]
= √632 / 3
σ = 14.51
تحديد وضع اللاجئ

الصيغة = (الانحراف المعياري / المتوسط) * 100
= (14.51 / 78) * 100
سيكون الانحراف المعياري -

RSD = 78 +/- 18.60٪
المثال رقم 2
يوضح الجدول التالي أسعار الأسهم XYZ. ابحث عن RSD لفترة 10 أيام.
المحلول:
فيما يلي بيانات لحساب الانحراف المعياري النسبي.

يعني
حساب المتوسط

μ = (53.73+ 54.08+ 54.14+ 53.88+ 53.87+ 53.85+ 54.16+ 54.5+ 54.4+ 54.3) / 10
μ = 54.091
الانحراف المعياري
لذلك ، يكون حساب الانحراف المعياري على النحو التالي ،

حساب الانحراف المعياري:
σ = 0.244027
تحديد وضع اللاجئ

الصيغة = (الانحراف المعياري / المتوسط) * 100
= (0.244027 / 54.091) * 100
سيكون الانحراف المعياري -

RSD = 0.451141
مثال الصيغة رقم 3
أجرت إحدى المؤسسات فحصًا صحيًا لموظفيها ووجدت أن غالبية الموظفين يعانون من زيادة الوزن ، وترد أدناه الأوزان (بالكيلوجرام) لـ 8 موظفين ، وأنت مطالب بحساب الانحراف المعياري النسبي.
المحلول:
فيما يلي بيانات لحساب الانحراف المعياري النسبي.

يعني
حساب المتوسط

μ = (130 + 120 + 140 + 90 + 100 + 160 + 150 + 110) / 8
μ = 125
الانحراف المعياري
لذلك ، يكون حساب الانحراف المعياري على النحو التالي ،

حساب الانحراف المعياري:
σ = 24.4949
تحديد وضع اللاجئ

الصيغة = (الانحراف المعياري / المتوسط) * 100
= (24.49490 / 125) * 100
سيكون الانحراف المعياري -

RSD = 19.6
نظرًا لأن البيانات عبارة عن عينة من السكان ، يجب استخدام صيغة تحديد وضع اللاجئ.
الصلة والاستخدام
يساعد الانحراف المعياري النسبي في قياس تشتت مجموعة من القيم فيما يتعلق بالمتوسط ، أي أنه يسمح لنا بتحليل الدقة في مجموعة من القيم. يتم التعبير عن قيمة RSD بالنسبة المئوية ويساعد على فهم ما إذا كان الانحراف المعياري صغيرًا أم ضخمًا عند مقارنته بمتوسط مجموعة من القيم.
المقام لحساب RSD هو القيمة المطلقة للمتوسط ولا يمكن أن يكون سالبًا. ومن ثم ، فإن تحديد وضع اللاجئ إيجابي دائمًا. يتم تحليل الانحراف المعياري في سياق المتوسط بمساعدة تحديد وضع اللاجئ. يستخدم RSD لتحليل تقلبات الأوراق المالية. تمكن RSD من مقارنة الانحراف في ضوابط الجودة للاختبارات المعملية.