صيغة القيمة P | أمثلة خطوة بخطوة لحساب القيمة الاحتمالية
ما هي صيغة القيمة P؟
P هو مقياس إحصائي يساعد الباحثين على تحديد ما إذا كانت فرضيتهم صحيحة. يساعد في تحديد أهمية النتائج. الفرضية الصفرية هي وضع افتراضي حيث لا توجد علاقة بين ظاهرتين تم قياسهما. يتم الإشارة إليها بواسطة H 0. الفرضية البديلة هي الفرضية التي قد تصدقها إذا تم التوصل إلى أن الفرضية الصفرية غير صحيحة. رمزها هو H 1 أو H a.
قيمة P في Excel هي رقم بين 0 و 1. توجد جداول وبرامج جداول بيانات وبرامج إحصائية للمساعدة في حساب القيمة p. مستوى الأهمية (α) هو عتبة محددة مسبقًا يحددها الباحث. بشكل عام هو 0.05. تشير القيمة الاحتمالية الصغيرة جدًا ، والتي تكون أقل من مستوى الأهمية ، إلى أنك ترفض الفرضية الصفرية. تشير القيمة P التي تزيد عن مستوى الأهمية إلى فشلنا في رفض الفرضية الصفرية.
شرح صيغة P-Value
يمكن اشتقاق معادلة حساب القيمة p باتباع الخطوات التالية:
حساب قيمة P من إحصاء Z.
الخطوة 1: نحتاج إلى معرفة إحصاء الاختبار z

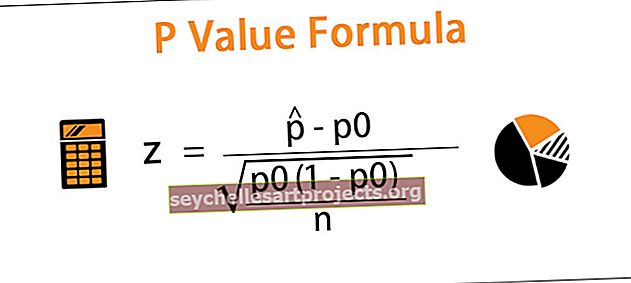
أين
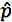 هو نسبة العينة
هو نسبة العينة- p0 هي نسبة السكان المفترضة في فرضية Null
- ن هو حجم العينة
الخطوة 2: نحتاج إلى إيجاد المستوى المقابل لـ p من قيمة z التي تم الحصول عليها. لهذا الغرض ، علينا النظر إلى جدول z.

المصدر: www.dummies.com
على سبيل المثال ، لنجد قيمة p المقابلة لـ z ≥ 2.81. بما أن التوزيع الطبيعي متماثل ، فإن قيم z السالبة تساوي قيمها الموجبة. 2.81 مجموع 2.80 و 0.01. انظر إلى 2.8 في العمود z والقيمة المقابلة البالغة 0.01. نحصل على p = 0.0025.
أمثلة على صيغة P-Value (مع قالب Excel)
دعونا نرى بعض الأمثلة البسيطة إلى المتقدمة لمعادلة P-Value لفهمها بشكل أفضل.
يمكنك تنزيل نموذج P Value Formula Excel من هنا - نموذج P Value Formula Excel
مثال 1
أ) القيمة الاحتمالية هي 0.3015. إذا كان مستوى الأهمية 5٪ ، فابحث عما إذا كان بإمكاننا رفض فرضية العدم.
ب) القيمة الاحتمالية هي 0.0129. إذا كان مستوى الأهمية 5٪ ، فابحث عما إذا كان بإمكاننا رفض فرضية العدم.
المحلول:
استخدم البيانات التالية لحساب القيمة الاحتمالية.

ستكون القيمة P -

أ) نظرًا لأن القيمة p 0.3015 أكبر من مستوى الأهمية 0.05 (5٪) ، فإننا نفشل في رفض فرضية العدم.
ب) نظرًا لأن القيمة p 0.0129 أقل من مستوى الأهمية 0.05 ، فإننا نرفض فرضية العدم.
المثال رقم 2
27٪ من الناس في الهند يتحدثون الهندية حسب دراسة بحثية. يشعر الباحث بالفضول لمعرفة ما إذا كان الرقم أعلى في قريته. ومن ثم ، فهو يضع إطارًا للفرضية الصفرية والبديلة. يختبر H 0: p = 0.27. ح أ: ف> 0.27. هنا ، p هي نسبة سكان القرية الذين يتحدثون الهندية. قام بإجراء مسح في قريته لمعرفة عدد الأشخاص الذين يمكنهم التحدث باللغة الهندية. وجد أن 80 من أصل 240 شخصًا في العينة يمكنهم التحدث باللغة الهندية. اكتشف القيمة الاحتمالية التقريبية لاختبار الباحث إذا افترضنا استيفاء الشروط اللازمة ومستوى الأهمية 5٪.
المحلول:
استخدم البيانات التالية لحساب القيمة الاحتمالية.

هنا ، حجم العينة ن = 240 ،
ص 0 هي نسبة السكان سيتعين علينا إيجاد نسبة العينة
= 80/240
 = 0.33
= 0.33
إحصاء Z
حساب إحصاء Z


= 0.33 - 0.27 / 0.27 * (1 - 0.27) / 240
إحصائية Z ستكون -

Z = 2.093696
ستكون قيمة P -

قيمة P = P (z ≥ 2.09)
علينا أن ننظر إلى قيمة 2.09 هي جدول z. لذلك ، علينا أن ننظر إلى -2.0 في العمود z والقيمة في العمود 0.09. بما أن التوزيع الطبيعي متماثل ، فإن المساحة على يمين المنحنى تساوي تلك الموجودة على اليسار. نحصل على القيمة p كـ 0.0183.
قيمة P = 0.0183
نظرًا لأن القيمة p أقل من المستوى المعنوي 0.05 (5٪) ، فإننا نرفض الفرضية الصفرية.
ملاحظة: في Excel ، تأتي القيمة p كـ 0.0181
المثال رقم 3
تشير الدراسات إلى أن الذكور يشترون عددًا أكبر من تذاكر الطيران مقارنة بالإناث. يتم شراؤها من قبل الذكور والإناث بنسبة 2: 1. تم إجراء البحث في مطار معين بالهند لمعرفة توزيع تذاكر الطيران بين الذكور والإناث. من بين 150 تذكرة ، تم شراء 88 تذكرة من قبل الذكور و 62 من الإناث. نحتاج إلى معرفة ما إذا كان التلاعب التجريبي يسبب التغيير في النتائج ، أم أننا نلاحظ تباينًا بالصدفة. احسب القيمة الاحتمالية بافتراض أن درجة الأهمية هي 0.05.
المحلول:
استخدم البيانات التالية لحساب القيمة الاحتمالية.

الخطوة 1: القيمة الملحوظة هي 88 للذكور و 62 للإناث.
- القيمة المتوقعة للذكور = 2/3 * 150 = 100 ذكر
- القيمة المتوقعة للإناث = 1/3 * 150 = 50 أنثى
الخطوة 2: اكتشف chi-square


= ((88-100) 2) / 100 + (62-50) 2/50
= 1.44 + 2.88
مربع تشي (X ^ 2)
مربع كاي (X ^ 2) سيكون -

مربع تشي (X ^ 2) = 4.32
الخطوة 3: ابحث عن درجات الحرية
نظرًا لوجود متغيرين - ذكور وإناث ، ن = 2
درجات الحرية = ن -1 = 2-1 =
الخطوة 4: من جدول القيمة p ، ننظر إلى الصف الأول في الجدول حيث أن درجة الحرية هي 1. يمكننا أن نرى أن قيمة p تتراوح بين 0.025 و 0.05. نظرًا لأن القيمة p أقل من درجة أهمية 0.05 ، فإننا نرفض فرضية العدم.
ستكون القيمة P -

قيمة P = 0.037666922
ملاحظة: يعطي Excel القيمة p مباشرة باستخدام الصيغة:
CHITEST (النطاق الفعلي ، النطاق المتوقع)
المثال رقم 4
من المعروف أن 60٪ من الأشخاص الذين يدخلون متاجر الملابس في مدينة ما يشترون شيئًا ما. أراد صاحب محل لبيع الملابس معرفة ما إذا كان الرقم أعلى لمتجر الملابس الذي يملكه. كان لديه بالفعل نتائج دراسة أجريت لمتجره. 128 من أصل 200 شخص دخلوا متجره قاموا بشراء شيء ما. أشار صاحب المحل إلى نسبة الأشخاص الذين دخلوا متجر الملابس الخاص به واشتروا شيئًا ما. كانت الفرضية الصفرية التي وضعها هو p = 0.60 وكانت الفرضية البديلة p> 0.60. أوجد القيمة الاحتمالية للبحث عند مستوى أهمية 5٪.
المحلول:
استخدم البيانات التالية لحساب القيمة الاحتمالية.

هنا ، حجم العينة n = 200. سيتعين علينا إيجاد نسبة العينة
= 128/200
 = 0.64
= 0.64
إحصاء Z
حساب إحصاء Z


= 0.64 - 0.60 / 0.60 * (1 - 0.60) / 200
إحصائية Z ستكون -

إحصاء Z = 1.1547
قيمة P = P (z ≥ 1.1547)
وظيفة NORMSDIST في Excel

سيكون NORMSDIST -

NORMSDIST = 0.875893461
توجد دالة مضمنة لحساب قيمة p من إحصاء az في Excel. تُعرف باسم دالة NORMSDIST. تحسب الدالة Excel NORMSDIST دالة التوزيع التراكمي العادي القياسي من القيمة المتوفرة. تنسيقه هو NORMSDIST (z). نظرًا لأن القيمة الإحصائية z موجودة في الخلية B2 ، فإن الوظيفة المستخدمة هي = NORMSDIST (B2).
ستكون قيمة P -

قيمة P = 0.12410654
نظرًا لأنه يتعين علينا إيجاد المساحة على يمين المنحنى ،
القيمة الاحتمالية = 1 - 0.875893 = 0.124107
نظرًا لأن قيمة p 0.124107 هي أكثر من مستوى مهم وهو 0.05 ، فإننا نفشل في رفض فرضية العدم.
الصلة والاستخدام
P-Value لها تطبيقات واسعة في اختبار الفرضيات الإحصائية ، وتحديداً في اختبار الفرضيات الصفرية. على سبيل المثال ، يدير مدير الصندوق صندوقًا مشتركًا. وهو يدعي أن العوائد من مخطط معين للصندوق المشترك تعادل Nifty ، وهو مؤشر سوق الأسهم القياسي. سيضع فرضية العدم القائلة بأن عوائد مخطط الصندوق المشترك تعادل عوائد شركة Nifty. ستكون الفرضية البديلة هي أن عائدات النظام وعوائد Nifty ليست متكافئة. ثم يقوم بحساب القيمة الاحتمالية.

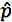 هو نسبة العينة
هو نسبة العينة